Предмет: Математика,
автор: Нурик203
Прошу вас, те кто в интегралах разбирается помогите
Использовать метод подстановки
Приложения:
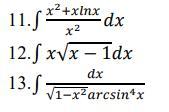
Ответы
Автор ответа:
1
Ответ: 11. x+1/2*ln²(x)+C, 12. 2/5*(x-1)^(5/2)+2/3*(x-1)^(3/2)+C, 13.-1/[3*arcsin³(x)]+C.
Пошаговое объяснение:
11. ∫[x²+x*ln(x)]*dx/x²=∫dx+∫ln(x)*dx/x=∫dx+∫ln(x)*d[ln(x)]. Полагая ln(x)=t, получим ∫[x²+x*ln(x)]*dx/x²=∫dx+∫t*dt=x+1/2*t²+C=x+1/2*ln²(x)+C.
12. Пусть x-1=t ⇒ dx=dt⇒∫x*√(x-1)*dx=∫(t+1)*√t*dt=∫t^(3/2)*dt+∫t^(1/2)*dt=2/5*t^(5/2)+2/3*t^(3/2)+C=2/5*(x-1)^(5/2)+2/3*(x-1)^(3/2)+C.
13. Так как dx/√(1-x²)=d[arcsin(x)], то ∫dx/[√(1-x²)*arcsin⁴(x)]=∫d[arcsin(x)]/arcsin⁴(x). Пусть arcsin(x)=t⇒∫dx/[√(1-x²)*arcsin⁴(x)]=∫dt/t⁴=-1/(3*t³)+C=-1/[3*arcsin³(x)]+C.
Похожие вопросы
Предмет: Русский язык,
автор: МаРьЯмКа2040
Предмет: Русский язык,
автор: DariaFly
Предмет: Русский язык,
автор: alexaynao89
Предмет: История,
автор: yablochkin2004
Предмет: Математика,
автор: настя04052007