Предмет: Алгебра,
автор: Аноним
Найдите область определения выражения:
Приложения:
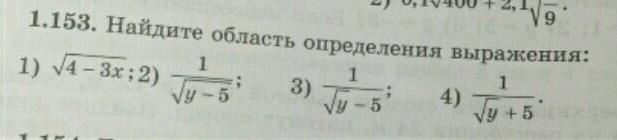
Ответы
Автор ответа:
2
Asan8654:
Помогите мне
В моем профиле самый последний вопрос
Мне срочно надо
там не переведено на русский язык...непонятно, что надо делать ...
Похожие вопросы
Предмет: Русский язык,
автор: annakwashko
Предмет: Английский язык,
автор: iuiiiazotova7
Предмет: Русский язык,
автор: vano2100
Предмет: Алгебра,
автор: oks2114222222
Предмет: Алгебра,
автор: ymycysym