Предмет: Математика,
автор: killberu
ДАЮ МНОГО БАЛЛОВ
Найти предел. Правилом Лапиталя пользоваться нельзя. Желательно решить через эквивалентность.з
Приложения:
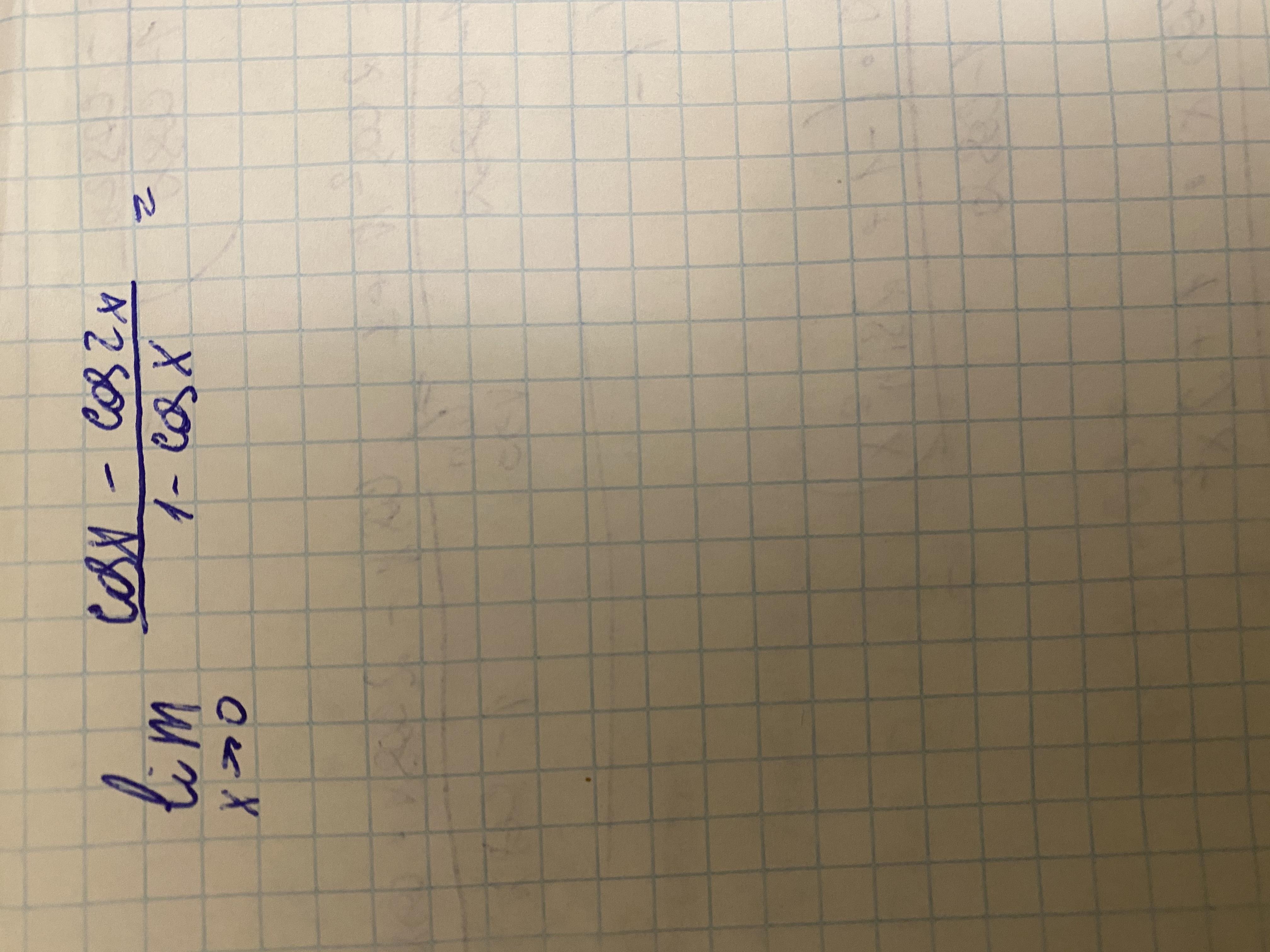
Ответы
Автор ответа:
0
Ответ:
3
Пошаговое объяснение:
Разложим в ряд тейлора cosx и cos2x до o(x^2)
получаем cosx = 1 - (x^2)/2 + o(x^2)
cos2x = 1 - ((2x)^2)/2 + o(x^2) = 1 - 2x^2 + o(x^2) (тут уже не совсем разложение в ряд тейлора, но так делать можно и нужно)
подставляем в предел:
lim(1-(x^2)/2 - (1 - 2x^2) + o(x^2))/(1 - (1 - (x^2)/2) + o(x^2)) = lim(3/2 * x^2 + o(x^2))/(1/2 * x^2 + o(x^2)) дальше делим всё на x^2 и получаем lim(3/2 + o(x^2))/(1/2 + o(x^2)) = 3/2 / 1/2 = 3
Похожие вопросы
Предмет: Русский язык,
автор: aleksandr00076
Предмет: Русский язык,
автор: skellkik
Предмет: Другие предметы,
автор: IsJaneIs
Предмет: Математика,
автор: Брат2017
Предмет: Математика,
автор: интересно17