Предмет: Алгебра,
автор: sadfgre23242
Помогите решить систему уравнений
Приложения:
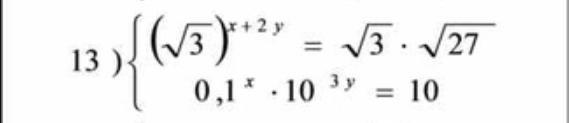
Ответы
Автор ответа:
0
Объяснение:
1).
2).
-х+3у=1
система
складываем 1-е и 2-е уравнения, получим систему уравнений:
Автор ответа:
1
Ответ:
(2; 1)
Объяснение:
...................................
Приложения:
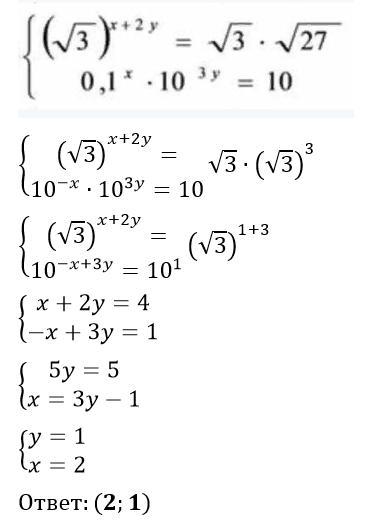
Похожие вопросы
Предмет: Русский язык,
автор: Алинчик2403
Предмет: Русский язык,
автор: анюта120912
Предмет: Русский язык,
автор: reohiug
Предмет: География,
автор: Danil7755