Предмет: Геометрия,
автор: fima1448857
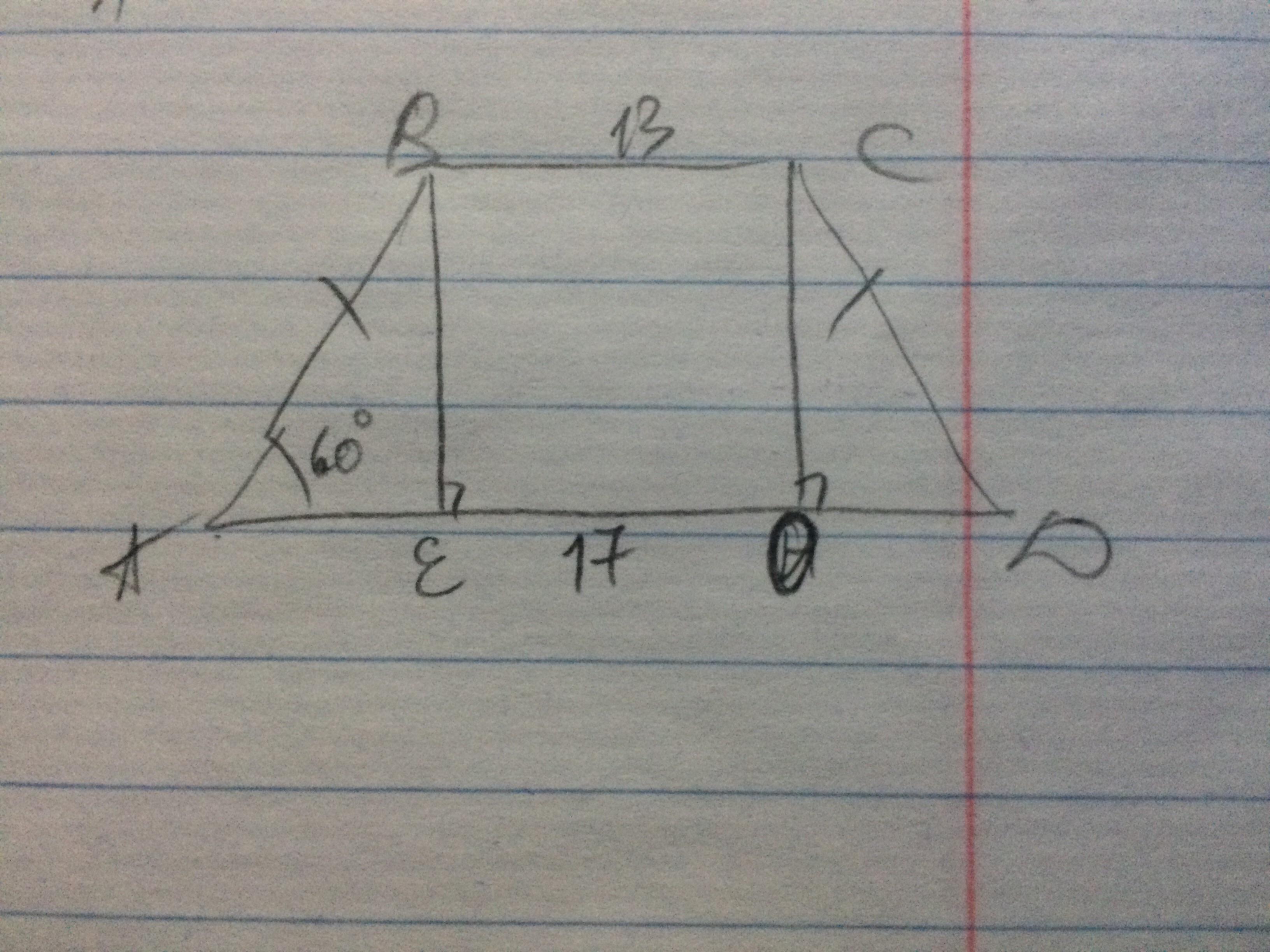
3. Найдите периметр равнобедренной трапеции, если её основания равны 13 и 17см, а угол при основании 60° умоляю пожалуйста.
Ответы
Автор ответа:
1
Ответ:
38см
Объяснение:
1. достроим высоты ВЕ и СО, тогда ВСОЕ - прямоуг(тк стороны попарно параллельны), следовательно ЕО=ВС=13см;
2. треуг АЕВ=треуг ДОС, по второму признаку равенства треугольников (УСУ):
угА=угД (тк трапеция равнобед);
АВ=СД (тк трапеция равнобед);
уг АВЕ=180-90-60=30 градусов=угДСО;
3. следовательно АЕ=ОД=(АД-ЕО):2=2см
4. рассм треуг АЕВ - прямоуг, тк ВЕ перпенд АД
уг АВЕ=180-90-60=30 градусов
АЕ = половине гипотенузы АВ , как катет против угла 30 градусов,
значит АВ = 2АЕ=2*2=4см
5. Р трапеции = 4+13+4+17=38см
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: daniilzubak01
Предмет: Русский язык,
автор: Tamindarovalov
Предмет: Русский язык,
автор: lizunicka130902
Предмет: Алгебра,
автор: ятакоголюбятвсегда
Предмет: Математика,
автор: Gydronkostya944