Предмет: Алгебра,
автор: qScorpion
2t⁴-16t³+31t²-8t+15=(t-3)*(2t⁴-10t²+t-5) помогите пожалуйста
Ответы
Автор ответа:
1
Ответ:
Надеюсь понятно решила
Приложения:
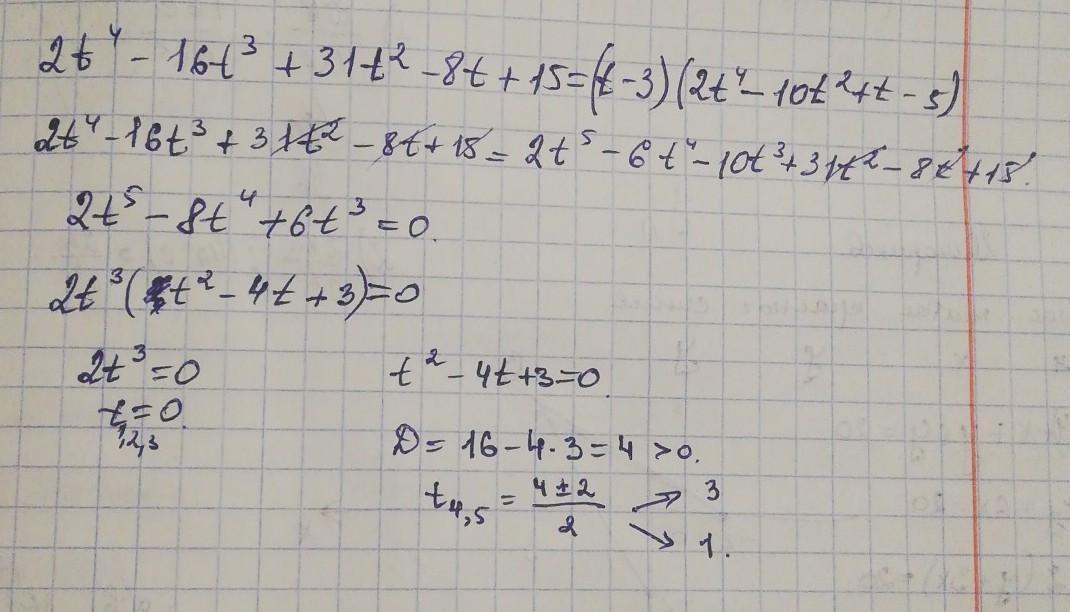
qScorpion:
Пасиба вам большое
Автор ответа:
4
Ответ:
(см. объяснение)
Объяснение:
Рассмотрим левую часть уравнения:
Тогда все уравнение примет вид:
Откуда корни уравнения:
Уравнение решено!
P.s: можно было просто раскрыть скобки в правой части уравнения и получить фразу . Далее вынести
за скобки и получить
. Такой прием решения тоже допустим.
Похожие вопросы
Предмет: Английский язык,
автор: selimovaziz
Предмет: Русский язык,
автор: mrluddit
Предмет: Русский язык,
автор: danaeremeeva
Предмет: Математика,
автор: cvanova