Предмет: Алгебра,
автор: angelinabyhmiller
помогите пожалуйста. Найдите коэффициент при Хн в разложении бинома Ньютона
Приложения:
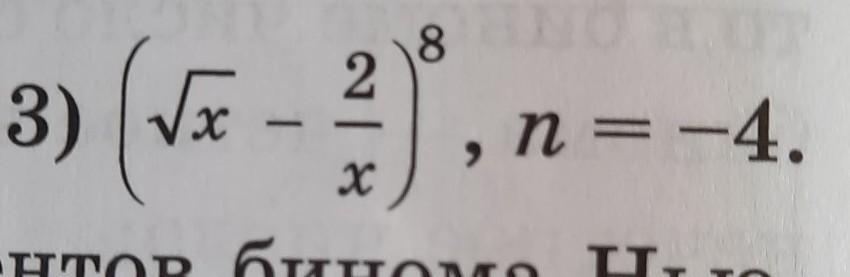
angelinabyhmiller:
можете этот выполнить и те два ещё?
Ответы
Автор ответа:
4
Показателя степени в разложении по биному Ньютона нет. Поэтому коэффициент перед
равен 0 .
Коэффициент перед равен 1 .
Похожие вопросы
Предмет: Русский язык,
автор: durnevanastya
Предмет: Английский язык,
автор: zairученик
Предмет: Русский язык,
автор: Ilovefcb1
Предмет: Математика,
автор: елена1138