Предмет: Геометрия,
автор: Raz3n
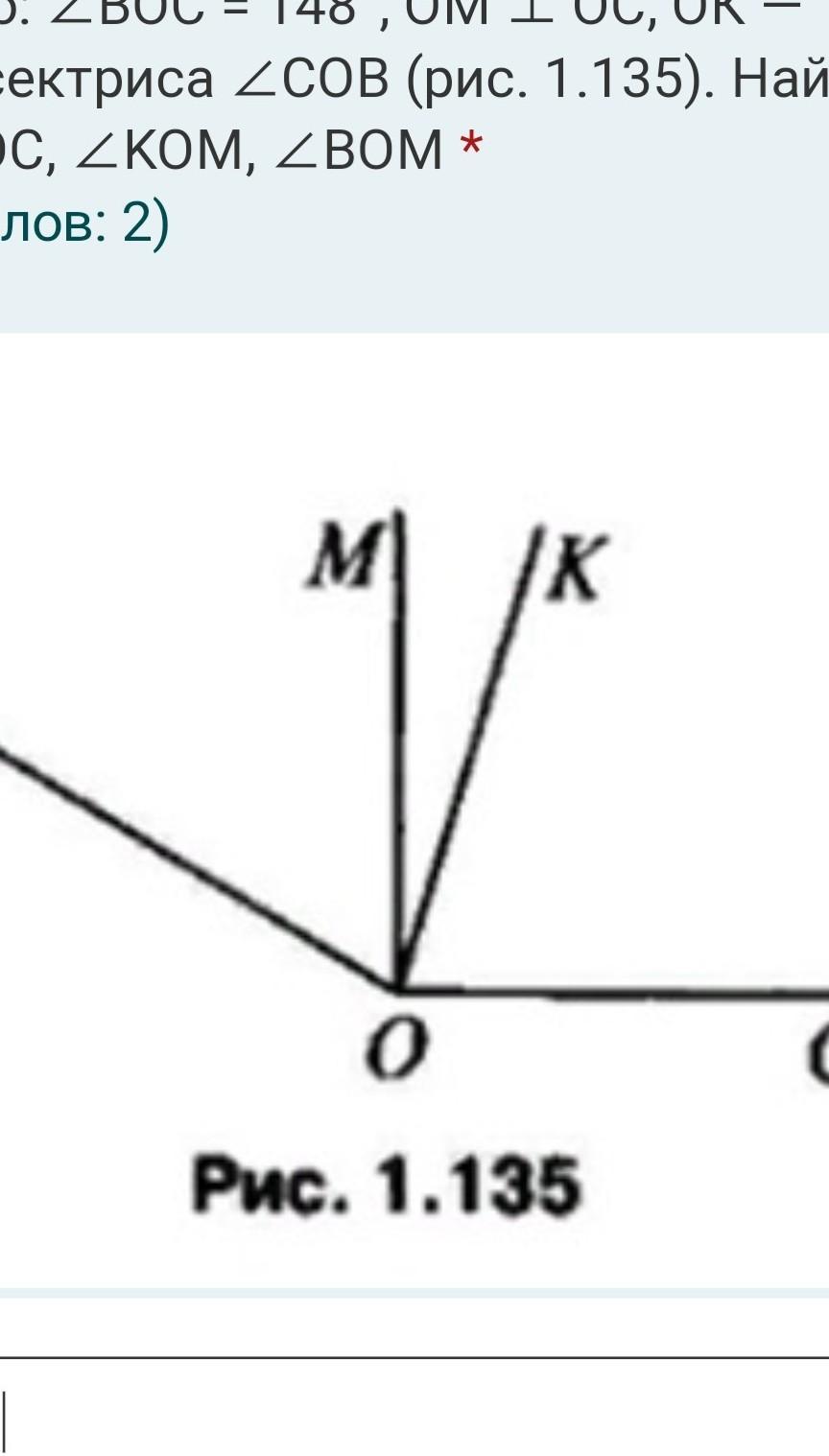
Дано: ∠BOC = 148°, ОМ ⊥ ОС, ОК — биссектриса ∠COB (рис. 1.135). Найти: ∠KOС, ∠KOM, ∠ВOM
Приложения:
Ответы
Автор ответа:
2
Ответ:
МОС=90º (т.к. МО перпендикулярнаОС)
КОС=148/2=74 º(ОК-бессектриса, а она делит угол на пополам)
Тогда получается: МОК=МОС-КОС
МОК= 90-74=16º
Похожие вопросы
Предмет: Русский язык,
автор: polinadovnorovi
Предмет: Русский язык,
автор: pom30
Предмет: Русский язык,
автор: amanda2090
Предмет: Математика,
автор: zuevkirill0
Предмет: Математика,
автор: Аноним