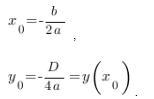Здравствуйте! Можете мне пожалуйста понятно объяснить как работают уравнения квадратичной функции и как их решать
Какие формулы нужны, как их правильно использовать, что с этим делать
Никак не могу разобраться, помощь очень нужна, спасибо!
Ответы
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. График квадратичной функции – парабола.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом(см. в приложении)
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
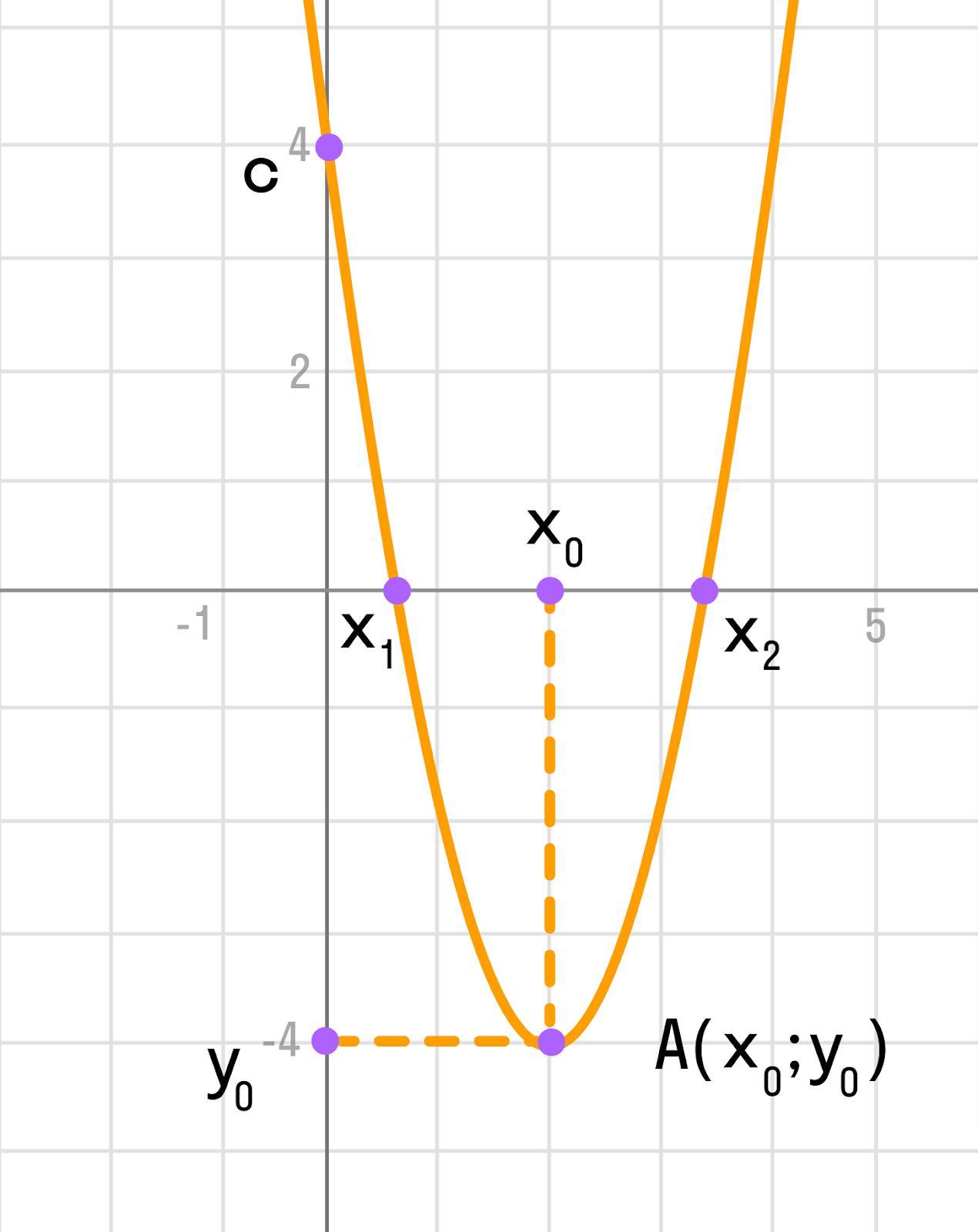
На изображении отмечены основные параметры графика квадратичной функции(также см приложение).
Разберем общий алгоритм на примере y = 2x2 + 3x - 5.
Как строим:
Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
Найдем дискриминант квадратного трехчлена 2x2 + 3x - 5.
D = b2 - 4ac = 9 - 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x - 5 = 0
Х1=-3+7/4=1
Х2=-3-7/4=-2,5
Подставляем полученные значения :
Х0=-b/2a=-3/4 =-0,75
Y0=D/4a=-49/8=-6,125
Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
Нанести эти точки на координатную плоскость и построить график параболы(см закреп)