Предмет: Алгебра,
автор: sumcovavarvara
помогите это срочно , дам много баллов
Приложения:
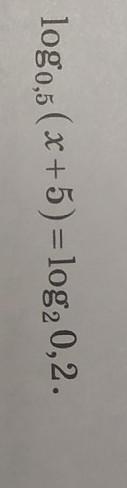
Ответы
Автор ответа:
0
Ответ:
x = 0
Объяснение:
ОДЗ:
При решении воспользуемся свойствами логарифма:
Тогда:
Логарифмы равны, а значит и подлогарифмические выражения равны:
Похожие вопросы
Предмет: Русский язык,
автор: Барзоава
Предмет: Русский язык,
автор: dashataylee
Предмет: Русский язык,
автор: hrvjhdgjtb
Предмет: Математика,
автор: morozowvlad
Предмет: Литература,
автор: Аноним