Предмет: Геометрия,
автор: cry79158
Пусть AK, BL, CN – биссектрисы треугольника ABC, I – точка их пересечения. Известно, что отношения площадей треугольников ANL, BKN и CLK к площади треугольника ABC равны, соответственно, 7/39, 9/65 и 7/15. Найдите отношение IK:AI.
siestarjoki:
Аналог: https://znanija.com/task/37834533
не понимаю((((
Ответы
Автор ответа:
6
Теорема о биссектрисе
IK/AI =BK/AB =CK/AC =x
IL/BI =AL/AB =CL/BC =y
IN/CI =BN/BC =AN/AC =z
Площади треугольников с равным углом
S(ANL)/S(ABC) =AN*AL/AB*AC =7/39 =yz
S(BKN)/S(ABC) =BK*BN/AB*BC =9/65 =xz
S(CLK)/S(ABC) =CL*CK/AC*BC =7/15 =xy
xy*xz/yz =x^2 =7/15 *9/65 *39/7 => x=3/5
IK:AI =3:5
Приложения:

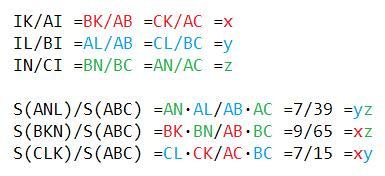
спасибо большое!
Похожие вопросы
Предмет: Українська мова,
автор: Nature12
Предмет: Английский язык,
автор: tzvetkovamaria
Предмет: Английский язык,
автор: imdarya
Предмет: Обществознание,
автор: gurginastya2003
Предмет: Физика,
автор: 3813090016