Question

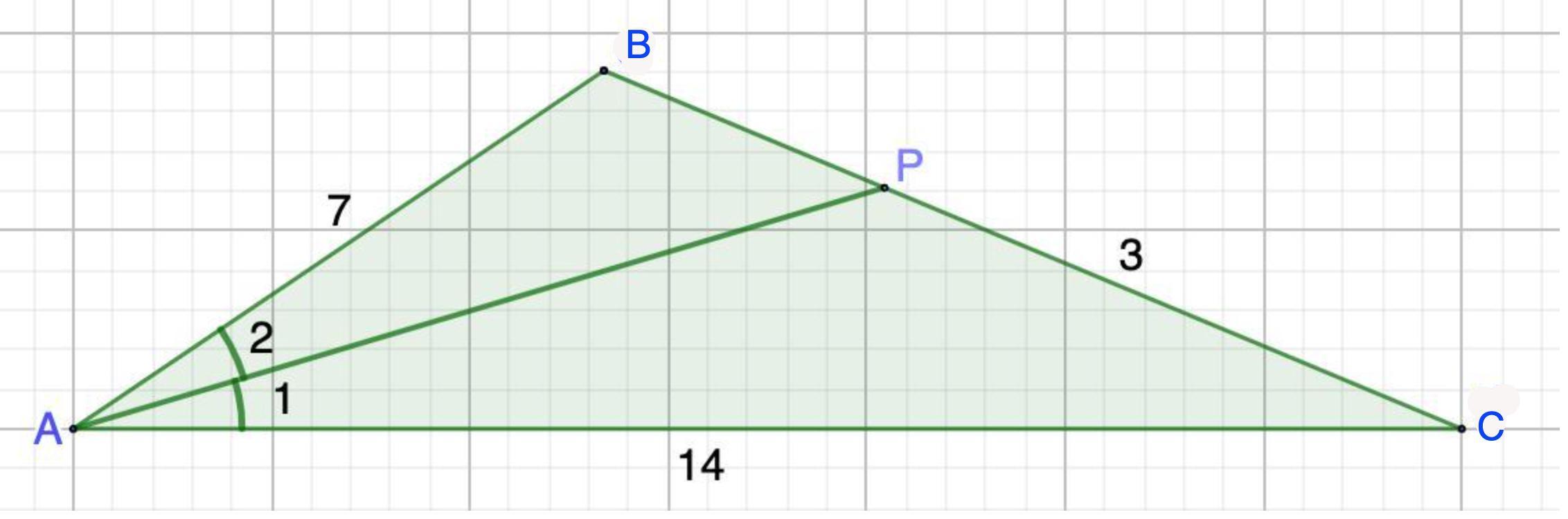
В треугольнике ABC проведена биссектриса AP. Известно, что AB=7, AC=14,
PC=3. Найдите BP

Answer 1

Ответ:

1,5 ед.

Объяснение:

Дано: ΔАВС.

АР - биссектриса;

АВ=7; АС=14; РС=3.

Найти: ВР.

Решение:

Биссектриса при вершине треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.

Составим пропорцию:

$\displaystyle \frac{PB}{AB} =\frac{PC}{AC}\\\\\frac{PB}{7}=\frac{3}{14}\\\\PB=\frac{7*3}{14}=\frac{21}{14}=\frac{3}{2}=1 \frac{1}{2}=1,5$

⇒ ВР = 1,5 ед.