Предмет: Математика,
автор: Dr01D
Решите СЛАУ матричным методом
Помогите пожалуйста
Приложения:
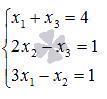
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
A · X = B
значит
X = A⁻¹ · B
Найдём обратную матрицу. Вычисляем алгебраические дополнения, вычеркиваем 1ю строку и 1й столбец
Выпишем союзную матрицу (матрицу алгебраических дополнений):
Теперь транспонированную союзную:
Найдем обратную матрицу:
Похожие вопросы
Предмет: Русский язык,
автор: nikserob
Предмет: Русский язык,
автор: 21242003
Предмет: Русский язык,
автор: zhivotovviktor
Предмет: Математика,
автор: карина2027