Предмет: Геометрия,
автор: blackname1
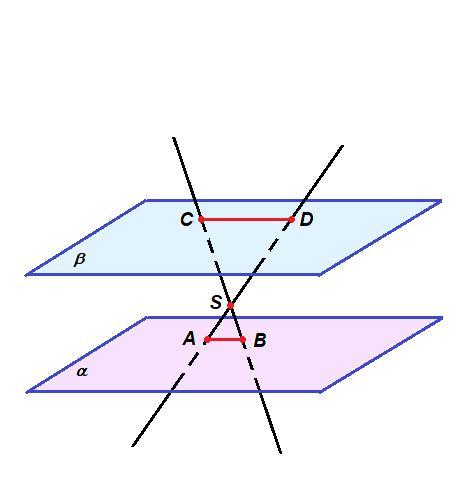
Плоскости α и β параллельны. Точки А и В принадлежат плоскости α, а точки С и D -
плоскости β. Отрезки АD и ВС пересекаются в точке S. Найти длину отрезка АВ, если
СD=3 см, СS=10 см, ВS=4 см.
Ответы
Автор ответа:
1
Ответ:
1,2 см
Объяснение:
Пересекающиеся прямые AD и ВС задают плоскость, которая пересекает плоскости α и β по прямым АВ и CD соответственно. А так как плоскости параллельны, то и линии пересечения их с третьей плоскостью параллельны.
AB ║ CD.
∠SAB = ∠SDC как накрест лежащие при пересечении АВ║CD секущей AD,
∠ASB = ∠DSC как вертикальные, ⇒
ΔASB ~ Δ DSC по двум углам.
см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: МаринаМиша
Предмет: Русский язык,
автор: sargisxachatry
Предмет: Русский язык,
автор: 110984maksim
Предмет: История,
автор: Аря55555
Предмет: История,
автор: Софуля12