Предмет: Геометрия,
автор: Avocadic1999
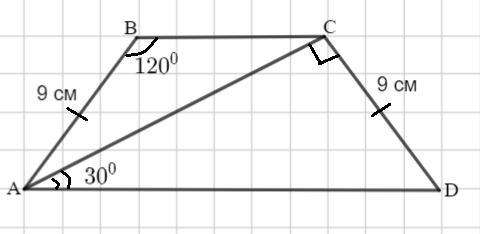
в равнобокой трапеции один из углов равен 120 градусов , диагональ трапеции образует с основанием 30 градусов . Найдите основания тропеции если ее боковая сторона равна 9 см
ПОМОГИТЕ ПОЖАЛУЙСТА СРОООЧНОО
Ответы
Автор ответа:
5
Ответ:
ВС=9 см, AD= 18 cм
Объяснение:
Рассмотрим трапецию ABCD -равнобедренную.
AB=CD =9см.
∠В=120°.
∠А и ∠В - внутренние односторонние при BC║ AD и секущей АВ.
Тогда ∠А + ∠В=180°.
Отсюда ∠ А=180°-120°=60°
Углы при основании равнобедренной трапеции равны ∠ A=∠D=60°.
По условию ∠ CAD= 30°.
∠ CAD=∠ BCA=30° как накрест лежащие при при BC║ AD и секущей АС.
∠ВАС=60°-30°=30°.
Тогда ∠ BCA=∠ВАС и Δ АВС - равнобедренный, так как в нем два угла равны.
Значит , ВС=АВ=9 см.
Рассмотрим треугольник ACD. ∠CAD= 30°, ∠ ADC= 60°.
Так как сумма углов треугольника равна 180°, то
∠ACD=180° -(30°+60°)=180°-90°=90°.
ΔACD - прямоугольный.
Так как катет лежит напротив угла в 30°, то
AD= 18 cм
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: gribkom
Предмет: Русский язык,
автор: sertyoq
Предмет: Русский язык,
автор: gorodeckaya8525
Предмет: Алгебра,
автор: ali220
Предмет: Алгебра,
автор: ololoshLee