Предмет: Математика,
автор: timchenkodima
помогите решить с полном решением
Приложения:
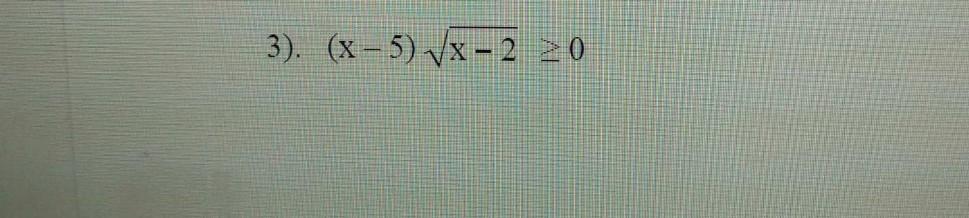
Ответы
Автор ответа:
0
Ответ:
[5;+∞)
Пошаговое объяснение:
ОДЗ:
Решение неравенства:
Найдем нули неравенства:
Построим числовую прямую, где отразим нули функции:
---------------------------------------------------
-∞ 2 5 +∞
Интервал (-∞;2) нас не интересует, так как не удовлетворяет ОДЗ
Проверим остальные, подставив любое число из интервала в неравенство:
1. Интервал [2;5) : не подходит.
2. Интервал [5;+∞) : подходит
Похожие вопросы
Предмет: Русский язык,
автор: linakhuainova
Предмет: Русский язык,
автор: anya5678
Предмет: Русский язык,
автор: olghavodkina
Предмет: Математика,
автор: aselya041
Предмет: Химия,
автор: svetlana264