Может ли при параллельном проецировании равнобедренной трапеции получиться прямоугольная трапеция?
Ответы
Параллельное проецирование: центр проецирования удалён в бесконечность, а проецирующие лучи параллельны между собой.
В декартовой системе координат возьмём 4 точки:
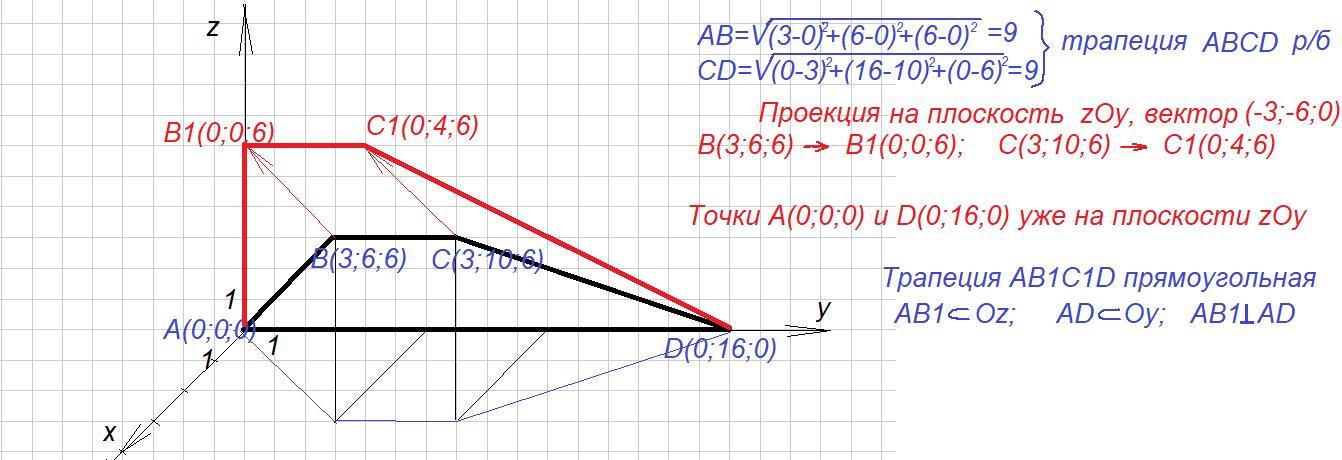
A(0;0;0), B(3;6;6), C(3;10;6) и D(0;16;0).
Рассмотрим векторы и
Векторы и
сонаправлены, то есть параллельны.
Через две параллельные прямые можно провести единственную плоскость, значит, ABCD - трапеция с основаниями
Боковые стороны трапеции равны: , значит, трапеция ABCD равнобедренная.
Проецируем трапецию ABCD на плоскость zOy по направлению вектора .
Точки A и D имеют нулевые абсциссы, значит, проекциями этих точек на плоскость zOy будут эти же точки.
Абсциссы точек В₁ и С₁ нулевые, то есть точки лежат в плоскости zOy.
Проекцией равнобедренной трапеции ABCD на плоскость zOy по направлению вектора является четырёхугольник AВ₁С₁D.
Проверим, является ли четырёхугольник AВ₁С₁D прямоугольной трапецией.
При параллельном проецировании сохраняется параллельность прямых:
Основание AD лежит на оси Oy, боковая сторона AB₁ лежит на оси Oz:
Четырёхугольник AB₁C₁D является прямоугольной трапецией с основаниями
Ответ: да, при параллельном проецировании равнобедренной трапеции может получиться прямоугольная трапеция.