Question

На боковой стороне AB трапеции ABCD (AD∥BC) отмечена середина M. Известно, что AD+BC=CD, ∠BAD=57∘, ∠MDA=51∘. Сколько градусов составляет угол BMC?

Answer 1

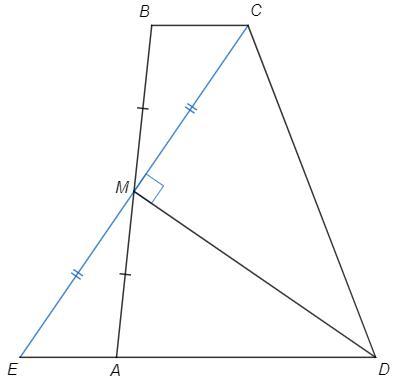
Продлим CM до пересечения с прямой AD в точке E.

BMC=AME (вертикальные), CBA=EAB (накрест лежащие при BC||AD)

△BMC=△AME (по стороне и прилежащим углам) => CM=EM, BC=AE

CD =AD+BC =AD+AE =ED

△CDE - равнобедренный => медиана DM является высотой, CMD=90  

BMD =BAD+MDA =57+51 =108 (внешний угол △AMD)

BMC =BMD-CMD =108-90 =18°