Предмет: Алгебра,
автор: Аноним
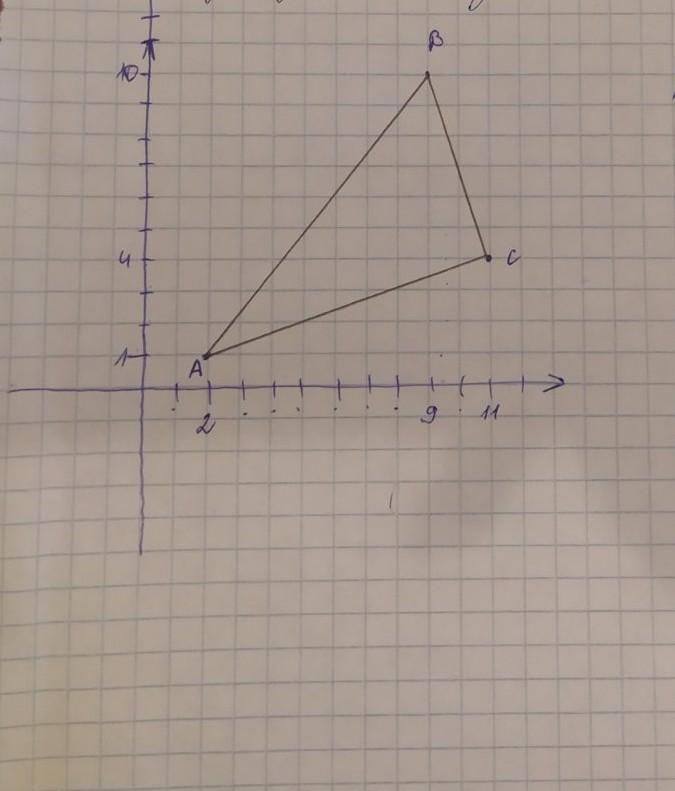
Найди периметр треугольника ABC, если его вершины имеют следующие координаты: A(2;1), B(9;10) и C(11;4).
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Найдем стороны треугольника как длины векторов:
Тогда периметр равен:
Автор ответа:
0
Ответ:
вот ответ на данную задачу
Приложения:

ПпапPpap145:
я крч забыла эту тему, так что удаляйте мой ответ
Похожие вопросы
Предмет: Русский язык,
автор: ladytoshkin
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Agatka
Предмет: Математика,
автор: varosyanerik