Предмет: Геометрия,
автор: BMiss1
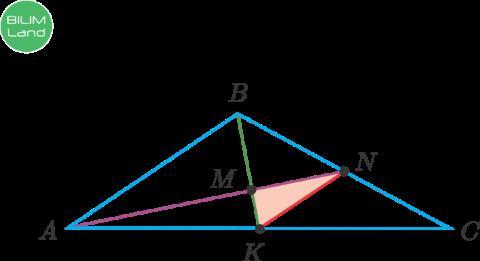
На рисунке BK и AN - это медианы треугольника ABC, AB = 30 см, BK = 15 см, AN = 36 см. Найдите периметр треугольника KMN.
Приложения:
Ответы
Автор ответа:
4
Ответ:
Р= 32 см.
Объяснение:
Так как BK и AN - медианы треугольника АВС, то точки K и N - середины сторон. Тогда отрезок KN - средняя линия.
Значит, средняя линия равна половине стороны АВ
KN =15 см.
Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
Тогда
MN= 12см.
MK=5 см.
Периметр треугольника - это сумма длин всех сторон треугольника.
Значит, Р= 32 см.
Похожие вопросы
Предмет: Русский язык,
автор: dasha271183
Предмет: Русский язык,
автор: milena2105
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: nastyabaraban
Предмет: Геометрия,
автор: 2407arinka