Предмет: Математика,
автор: fifbinkukil
прошу помогите, просто срочно нужно!!! Можете хотя-бы попытаться хоть если будет и не правильно по благодарю
Приложения:
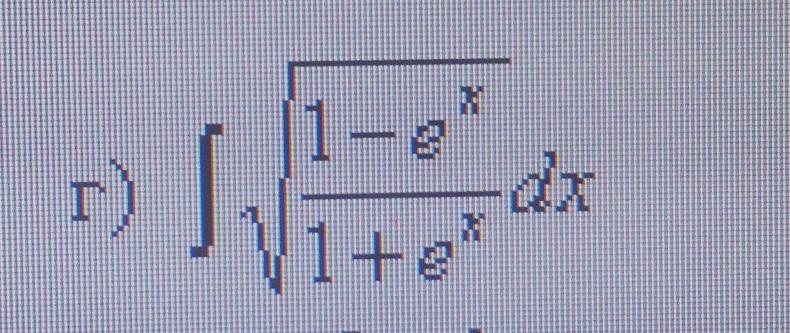
Ответы
Автор ответа:
1
Ответ:
вот что у меня получилось
Приложения:
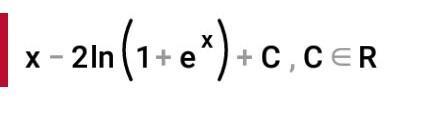
fifbinkukil:
ясно
кстати а в фотомасе нет тип история решенных задач
просто он у меня есть
быть может он у тебя сохранился?)
спс, нашёл)
вообще то спс тебе), ну да ладно
я про историю сохранения в фотомас)
аа
все я кстати чекнул
рахмет
Автор ответа:
0
Ответ:
Пошаговое объяснение:
=
подстановка
ещё замена
разложим на дроби
Получили табличные интегралы
обратная замена
Похожие вопросы
Предмет: Русский язык,
автор: tanyazvezda47
Предмет: Українська мова,
автор: rostislav555
Предмет: Русский язык,
автор: yby24
Предмет: Математика,
автор: Glazkovanuriya
Предмет: Алгебра,
автор: делюна0