Предмет: Математика,
автор: patriot2004
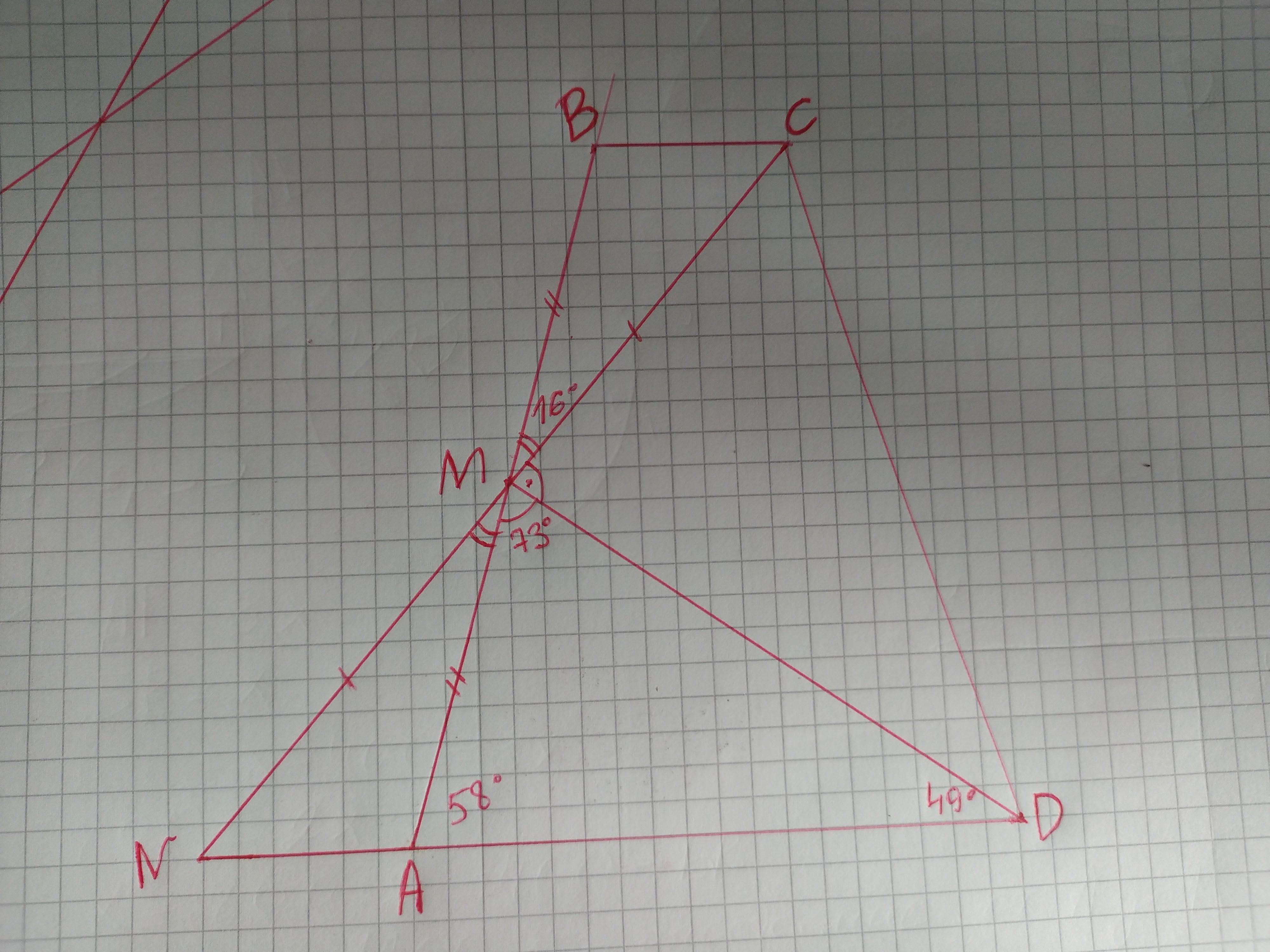
На боковой стороне AB трапеции ABCD (AD∥BC) отмечена середина M. Известно, что AD+BC=CD, ∠BAD=58∘, ∠MDA=49∘. Сколько градусов составляет угол BMC?
siestarjoki:
https://znanija.com/task/39226807
Ответы
Автор ответа:
6
Пусть MN и AD пересекаются в точке N
Рассмотрим треугольники NAM и MCB:
т. М - середина АВ ⇒ АМ=МВ;
СN ∦ ВС и ND ⇒∠ВСМ =∠МАN (накрест лежащие)
⇒ΔNAM ≅ ΔMCB (по ΙΙ признаку)
⇒NM=MC;
NA=BC
CD = AD+BC = NA+AD⇒CD=ND
⇒ΔNDC равнобедренный, тогда DM - его высота
∠DMC=90°
∠DMA = 180° - (∠DAM+∠ADM) = 180°-(58°+49°) =180°-107° =73°
∠NMA=∠CMB = 180° - (∠AMD+∠DMC) = 180°-(73°+90°) =180°-163° =17°
∠CMB=17°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: jeka930909
Предмет: Русский язык,
автор: elenamaslova815
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: ооощаопоказ