Предмет: Алгебра,
автор: vipsergazyev
Помогите плиз, 15 баллов, дифференциал
Приложения:
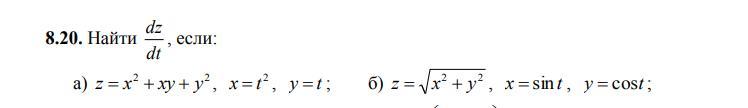
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Английский язык,
автор: elizad
Предмет: Английский язык,
автор: kifanidi
Предмет: Русский язык,
автор: крит1
Предмет: Алгебра,
автор: цветок68