Предмет: Математика,
автор: elmir2002isma
вычислите площадь фигуры, ограниченной линиями: только 9 Вариант пожалуйста
Приложения:
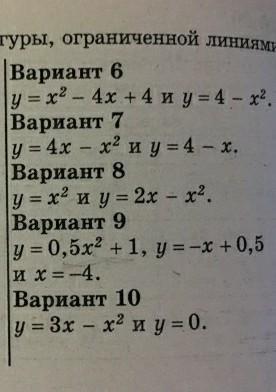
Ответы
Автор ответа:
1
Условие:
Вычислить площадь фигуры, ограниченной линиями:
Решение:
Такая фигура называется криволинейной трапецией, а ее площадь находится по следующей формуле:
Ограничивающие функции y₁(x) и y₂(x), а также левая граница интервала a = -4 нам известны по условию задачи. Чтобы найти правую границу b приравняем функции y₁(x) и y₂(x) и решим уравнение.
Таким образом правая граница b = -1 найдена.
Найдем интеграл
Ответ: S = 4,5
Похожие вопросы
Предмет: Русский язык,
автор: asanov1999
Предмет: Русский язык,
автор: chatrow
Предмет: Русский язык,
автор: Suleimanova54
Предмет: Математика,
автор: asamenssilavuowudxd
Предмет: Математика,
автор: Marinap04174