Предмет: Геометрия,
автор: kira10111990
30 баллов
Одна из двух равных окружностей проходит через центр другой окружности.
Вычисли длину общей хорды, если радиус окружности равен 12 м.
Ответ: длина общей хорды равна
−−−−−√ м.
№2
Дано, что tgα=7/24. Определи синус этого угла.
Ответ: sinα=
(дробь не сокращай).
Приложения:
Ответы
Автор ответа:
2
Ответ:
1. 12√3 м
2.
Объяснение:
1.
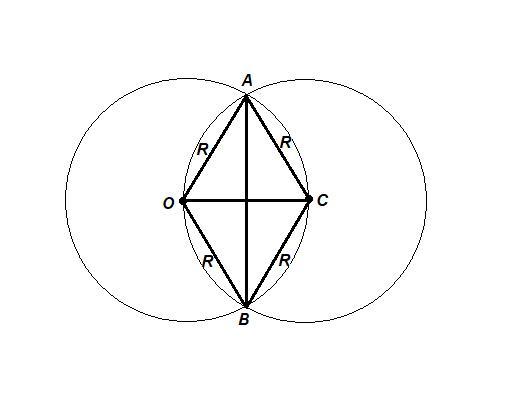
Даны две окружности одинакового радиуса R = 12 м, с центрами О и С.
АВ - общая хорда.
Тогда равны отрезки:
ОА = ОВ = СА = СВ = ОС = R = 12 м
ОАСВ - ромб.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. И так как стороны ромба равны, получаем:
AB² + OC² = 4 · OA²
AB² + R² = 4R²
AB² = 3R² = 3 · 12²
AB = 12√3 м
2.
Основное тригонометрическое тождество:
,
если в задаче угол α меньше развернутого.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Лизуша1177
Предмет: Русский язык,
автор: piccolotoppoli
Предмет: Русский язык,
автор: радостьмоя
Предмет: Математика,
автор: полина55555557