Предмет: Математика,
автор: nikitik
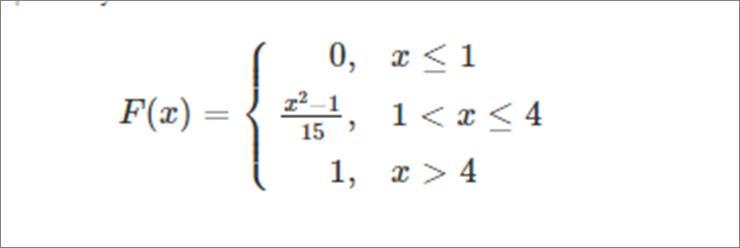
Дана функция распределения некоторой случайной величины:
Найдите математическое ожидание.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: artemkravchenko
Предмет: Русский язык,
автор: amirratmir
Предмет: Русский язык,
автор: EeOneGuy1234
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: aldik2033