Question

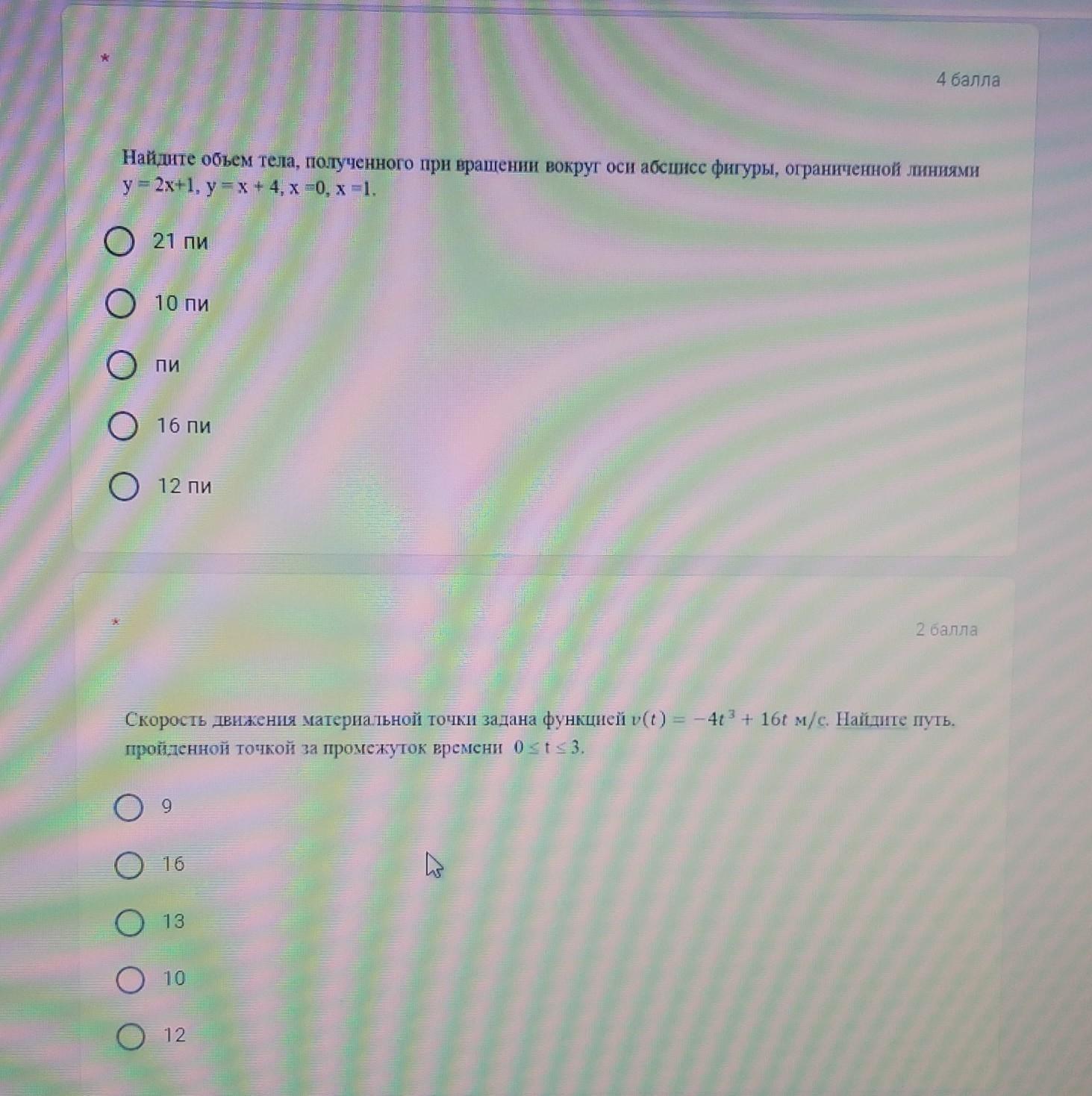
алгебра срочно помогите пожалуйста ​

Answer 1

Ответ:

1) 16π

2) 9

Объяснение:

1)

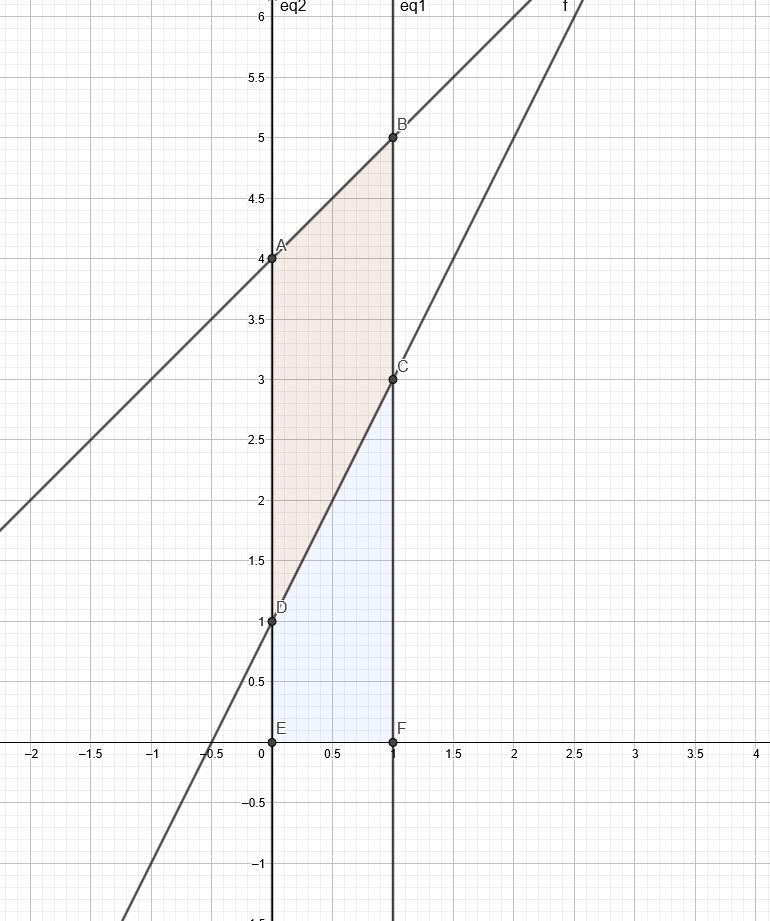
Нарисуем сначала графики функций

$y=2x+1\\y=x+4\\x=0\\x=1$

см. рисунок

Нам необходимо найти объем тела вращения закрашенного красным, мы его будем находить как объем тела вращения всего (и красного, и синего) минус объем синего.

Найдем общий объем

Конечно же мы знаем формулу для нахождения объема тела вращения ограниченной точками а и b и функцией f(x) - это

$\displaystyle \pi\int\limits^a_b {f(x)^2} \, dx$

Тогда найдем объем всего тела (и красного, и синего) - ограничены функцией y = x + 4, пределы от 0 до 1

$\displaystyle \pi\int\limits^a_b {f(x)^2} \, dx=\pi\int\limits^1_0 {(x+4)^2} \, dx=\pi\int\limits^1_0 {x^2} \, dx+\pi\int\limits^1_0 {8x} \, dx+\pi\int\limits^1_0 {16} \, dx=\pi \frac13x^3\Bigg|^1_0+4\pi x^2\Bigg|^1_0+16\pi x\Bigg|^1_0=\frac13\pi+4\pi+16\pi$

И найдем объем просто синего - ограничен функцией y = 2x + 1, пределы - от 0 до 1

$\displaystyle \pi\int\limits^a_b {f(x)^2} \, dx=\pi\int\limits^1_0 {(2x+1)^2} \, dx=\pi\int\limits^1_0 {4x^2+4x+1} \, dx=\pi\int\limits^1_0 {4x^2} \, dx+\pi\int\limits^1_0 {4x} \, dx+\pi\int\limits^1_0 {1} \, dx=\frac43\pi x^3\Bigg|^1_0+2\pi x\Bigg|^1_0+\pi x\Bigg|^1_0=\frac43\pi+2\pi+\pi$Вычтем из первого объема второй, чтобы найти нужный нам объем

$\displaystyle \frac13\pi+4\pi+16\pi-\frac43\pi-2\pi-\pi=16\pi$

ОТВЕТ: $16 \pi$

2)

Давайте вспомним, что такое путь:

$S=v*t=v(t)*t$

Таким образом, мы можем выразить путь как площадь под графиком скорости от времени

$\displaystyle S=\int\limits^a_bv(t)dv$

Пределы у нас известны, функция v(t) тоже. Тогда пишем и интегрируем

$\displaystyle S=\int\limits^a_bv(t)dt=\int\limits^3_0(-4t^3+16t)dt=\int\limits^3_0-4t^3dt+\int\limits^3_016tdt=-t^4\Bigg|^3_0+8t^2\Bigg|^3_0=8*3^2-4*3^3=-9$

так как путь не должен быть отрицателен, берем по модулю

ОТВЕТ: 9