Question

В равнобедренной трапеции диагональ, равная 4 см, составляет с основанием угол 60°. Найдите среднюю линию трапеции.
Пожалуйста объясните как делать эту парашу ​

Answer 1

Ответ:

2 см

Объяснение:

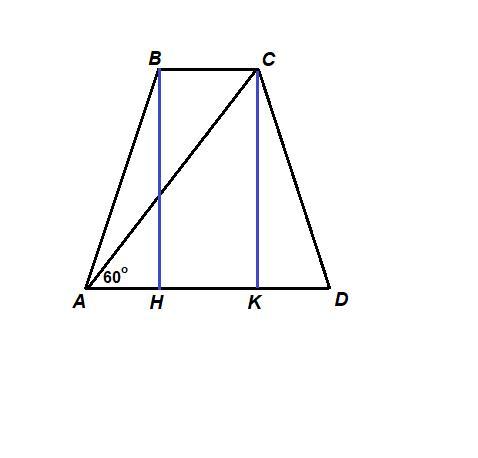
Проведем ВН и СК - высоты.

НВСК - прямоугольник, так как все углы прямые,

НК = ВС.

ΔАВН = ΔDCK по гипотенузе и катету:

• ∠АНВ = ∠DKC = 90°,
• АВ = CD, так как трапеция равнобедренная,
• ВН = СК как высоты трапеции.

Значит, АН = DK.

$AH=DK=\dfrac{AD-HK}{2}=\dfrac{AD-BC}{2}$

$AK=AH+HK=\dfrac{AD-BC}{2}+BC=$

$=\dfrac{AD-BC+2BC}{2}=\dfrac{AD+BC}2$

То есть, получили, что отрезок АК равен полусумме оснований.

Но средняя линия (m) тоже равна полусумме оснований:

$m=\dfrac{AD+BC}{2}=AK$

ΔACK:  ∠AKC=90°,   ∠CAK = 60°, значит ∠АСК = 30°,

АК = 1/2 АС = 1/2 · 4 = 2 см по свойству катета, лежащего против угла в 30°.

m = AK = 2 см