Предмет: Алгебра,
автор: au456
Исследовать сходимость ряда по признакам сравнения
Приложения:
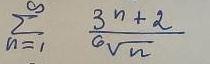
Ответы
Автор ответа:
1
Минорантный ряд расходится, значит по признаку сравнения расходится и мажорантный ряд
.
Похожие вопросы
Предмет: Английский язык,
автор: IkochetovaI
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: sus1
Предмет: Математика,
автор: МарияЕрг
Предмет: Математика,
автор: KENIyt