Предмет: Математика,
автор: DJRespecT
Докажите, что
| z₁ + z₂ |² + | z₁ − z₂ |² = 2*| z₁ |² + 2*| z₂ |²
для случайного z₁, z₂ ∈ C.
Приложения:
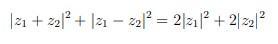
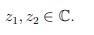
Ответы
Автор ответа:
1
Ч.т.д.
_______________
Использованные св-ва:
Похожие вопросы
Предмет: Русский язык,
автор: Аличка21062002
Предмет: Русский язык,
автор: lika84
Предмет: Русский язык,
автор: nikitkaafanasenir
Предмет: Математика,
автор: хждбьт
Предмет: Геометрия,
автор: crazyspace