Question

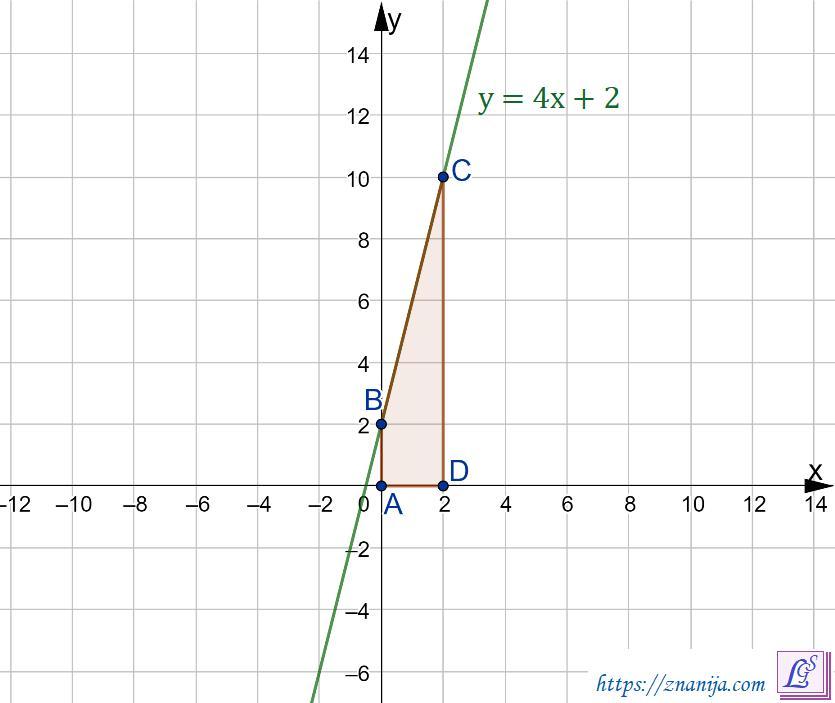
Вычислить площадь криволинейной трапеции, ограниченной линиями y=4x+2; x=0, x=2

Answer 1

Ответ:

Площадь криволинейной трапеции равна 12 кв. ед.

Пошаговое объяснение:

Площадь криволинейной трапеции найдем по формуле Ньютона-Лейбница:

$\displaystyle S = \int_a^b f(x )dx = F(x) |_a^b=F(b)-F(a)$

График прилагается.

$\displaystyle S_{ABCD} = \int_0^2 (4x+2)dx =\int_0^2 4xdx+\int_0^2 2dx =\\\\=( \frac{4x ^{2} }{2} +2x)|_0^2 =(2x ^{2}+2x)|_0^2= \\\\ =(2*2^{2} +2*2)-(2*0^{2} +2*0) = 12+0=12$

Площадь криволинейной трапеции равна 12 кв. ед.