Question

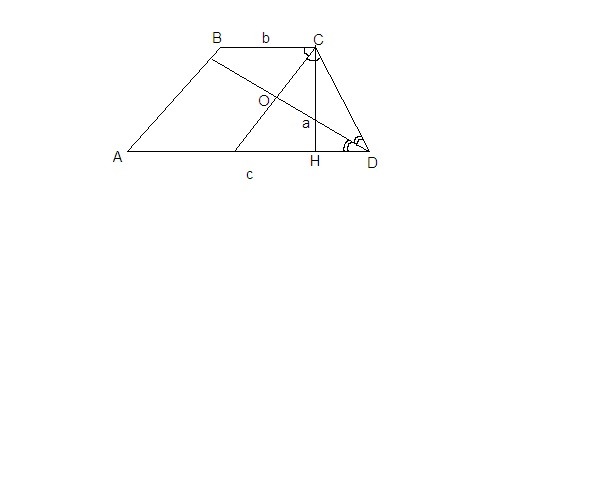
В трапеции ABCD, AD – большее основание, угол D = 60°. Биссектрисы углов C и D пересекаются в точке О, ОD = а, ВС = в, AD = с. Найдите площадь трапеции.

Answer 1

Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.
∠BCD + ∠CDA = 180°,  значит сумма их половинок равна 90°,
∠OCD + ∠ODC = 90°, ⇒ ∠COD = 90°, ∠CDO = 30°.

Проведем высоту СН.
ΔCHD: ∠CHD = 90°, ∠CDH = 60°, ⇒ ∠HCD = 30°
            
ΔCHD = ΔDOC по гипотенузе и острому углу (CD - общая гипотенуза, ∠HCD = ∠CDO = 30°), ⇒
CH = DO = a

Sabcd = (b + c)/2 · a