логарифмы. 6.12 (б), 6.13 (б), 6.15 (а).
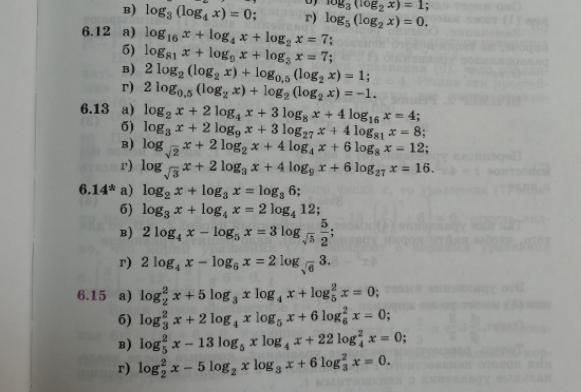
Ответы
Ответ:
6.12
log3^4(x)+log3^2(x)+log3(x)=7
1/4*log3(x)+1/2*log3(x)+log3(x)=7
7/4*log3(x)=7
log3(x)=4
x=3^4
x=81
6.13
log3(x)+2*log3^2(x)+*log3^3(x)+4*log3^4(x)=8
log3(x)+2*1/2*log3(x)+3*1/3*log3(x)+4*1/4+log3(x)=8
log3(x)+log3(x)+log3(x)+log3(x)=8
4*log3(x)=8
log3(x)=2
x=3^2
x=9
6.15
log2(x)^2-5log2(x)* log2(x)/log2(3) +6* (log2(x)/log2(3))^2 =0
log2(x)^2 -5*log2(x)^2/log2(3) +6*log2(x)^2/log2(3)^2=0
log2(x)^2=0
log2(x)=0
x=1
6.12(б)
log₈₁x+log₉(x)+log₃x=7
ОДЗ х>0,
по правилу перехода к новому основанию перейдем к основанию 3
log₃x/log₃81+log₃x/log₃9+log₃x=7; приведем к общему знаменателю и воспользуемся определением логарифма.
log₃x/4+log₃x/2+log₃x=7
7*log₃x=28
log₃x=4; х=81∈ОДЗ.
x=81
6.13(б)
log₃x+2*log₉x*log₂₇x+4*log₈₁x=8
ОДЗ х∈(0;+∞), на этом множестве можно упростить уравнение.
log³x+2*0.5*log₃x+3*(1/3)*log₃x+4*(1/4)*log₃x=8
log₃x=8/4
log₃x=2
x=3²
x=9∈ОДЗ
х=9
6.15(а)
log²₂x+(5/2)(log₂x/log₂3)* log₂x+ (log²₂х)/log²₂3 =0
log²₂x*(1+(5/(2log₂3) +1/log²₂3 )=0
(1+(5/(2log₂3) +1/log²₂3 )≠0
log²₂x=0
log₂x=0
х=2⁰
x=1∈ОДЗ
х=1