Предмет: Математика,
автор: erty901
Исследовать функции на непрерывность в указанных точках
Приложения:
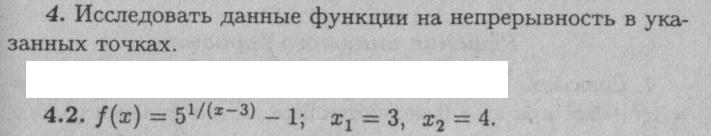
Ответы
Автор ответа:
10
Ответ:
Пошаговое объяснение:
Давайте вспомним определение непрерывности.
Определение Если функция непрерывна в точке
, то
.
Проверим функцию на непрерывность в точке 3.
Отсюда следует, что в точке 3 данная функция не является непрерывной
Проверим функцию на непрерывность в точке 4.
Отсюда следует, что в точке 4 данная функция является непрерывной
Похожие вопросы
Предмет: Английский язык,
автор: Сергей0196
Предмет: Русский язык,
автор: Tadeva00
Предмет: Русский язык,
автор: KrIsTinKa17
Предмет: География,
автор: juliamolchanov2
Предмет: Математика,
автор: mindumelena