Периметр боковой грани правильной треугольной призмы равен 12 см. При какой длине стороны основания призмы ее объем будет наибольшим?
Ответы
Ответ:
2
Пошаговое объяснение:
Пусть одна из сторон основания такой призмы - х, и ее высота - h. Тогда периметр ее боковой стороны - и он равен 12.
Найдем объём такой призмы.
Объем призмы - площадь основания (в данном случае треугольника) умноженный на высоту (h)
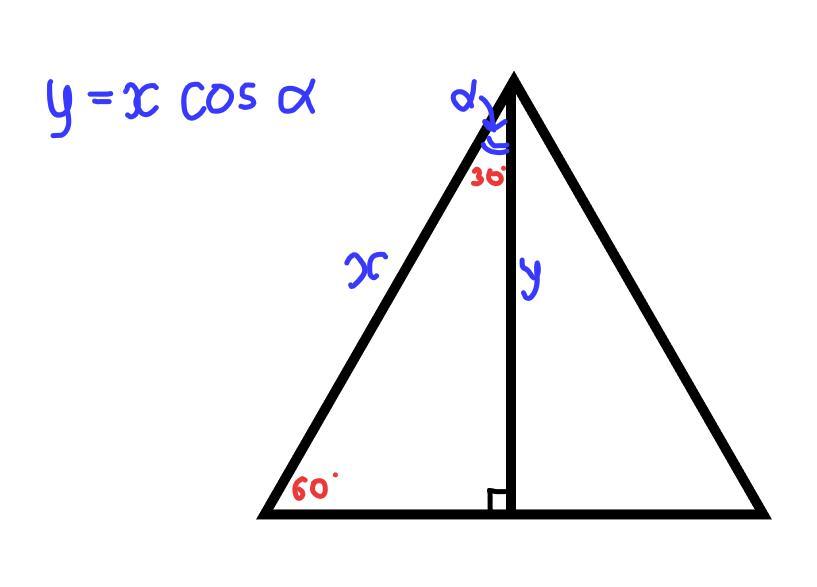
Найдём площадь треугольника в основании (см. рис. 1.)
1) проведём высоту у. Тогда площадь этого треугольника будет равна
После проведения высоты у нас оказался прямоугольный треугольник со сторонами x и y, и углом между ними в 30°
Тогда его площадь -
Выразим h через х:
Подставим в формулу объема:
Найдём экстремумы функции:
1) Найдем производную:
Приравняем её к 0
Поскольку у нас геометрия и таких страшных штук как отрицательные стороны у нас нет. Осталось только выбрать между 2 и 0.
Если 0, то это вообще не призма, знак производной говорит тоже самое.
Тогда подходит 2.
И это ответ!