Предмет: Алгебра,
автор: JLeuTeHaHT
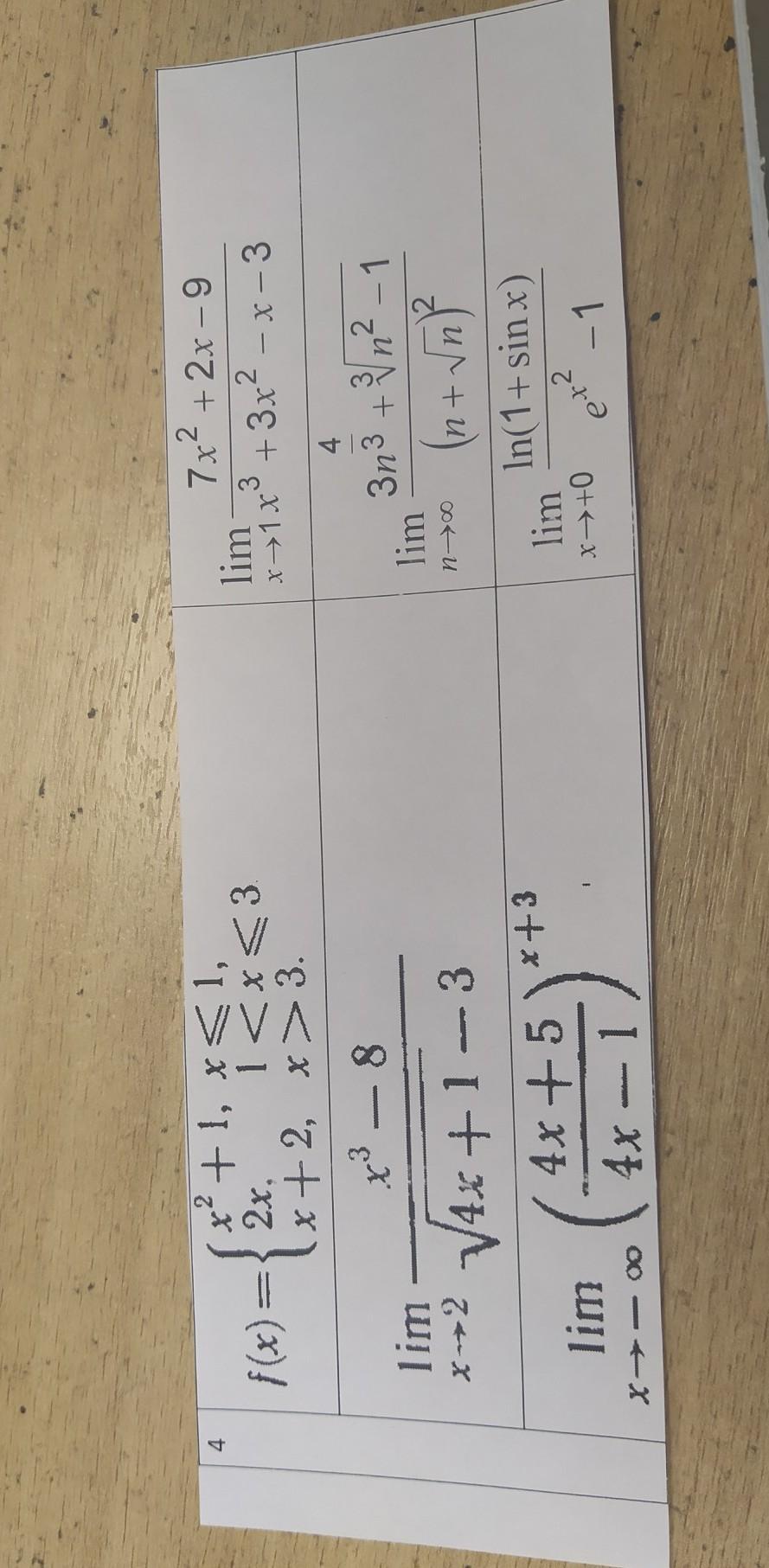
пределы первый столбец 3, второй столбец 2,3
Приложения:
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: gjgbjfv
Предмет: Английский язык,
автор: remvasilenko
Предмет: Английский язык,
автор: gjgbjfv
Предмет: Биология,
автор: ЯзьПомогитэ