Предмет: Алгебра,
автор: javohirhello
Дайте развёрнутое решение к упражнению на картинке
Приложения:
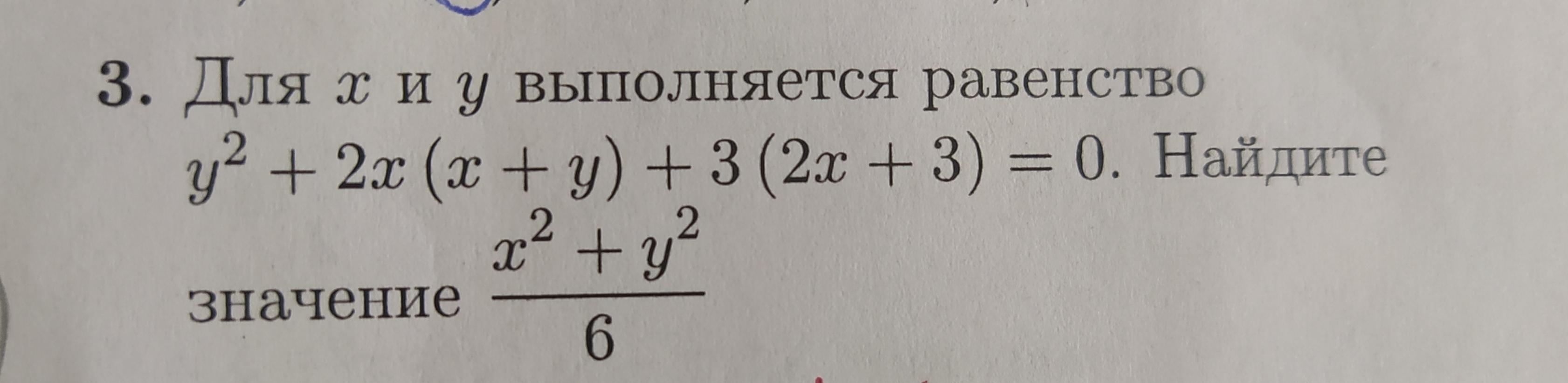
Ответы
Автор ответа:
2
Сумма квадратов ( неотрицательных выражений: и
) может равняться 0 только в случае равенства нулю каждого слагаемого.
Похожие вопросы
Предмет: Английский язык,
автор: mikhignatov201
Предмет: Русский язык,
автор: klepa06
Предмет: Английский язык,
автор: anyapotockaya
Предмет: Алгебра,
автор: kotik216