Предмет: Алгебра,
автор: natalia2810
Решить тригонометрические неравенства, напишите на листике если несложно
Приложения:
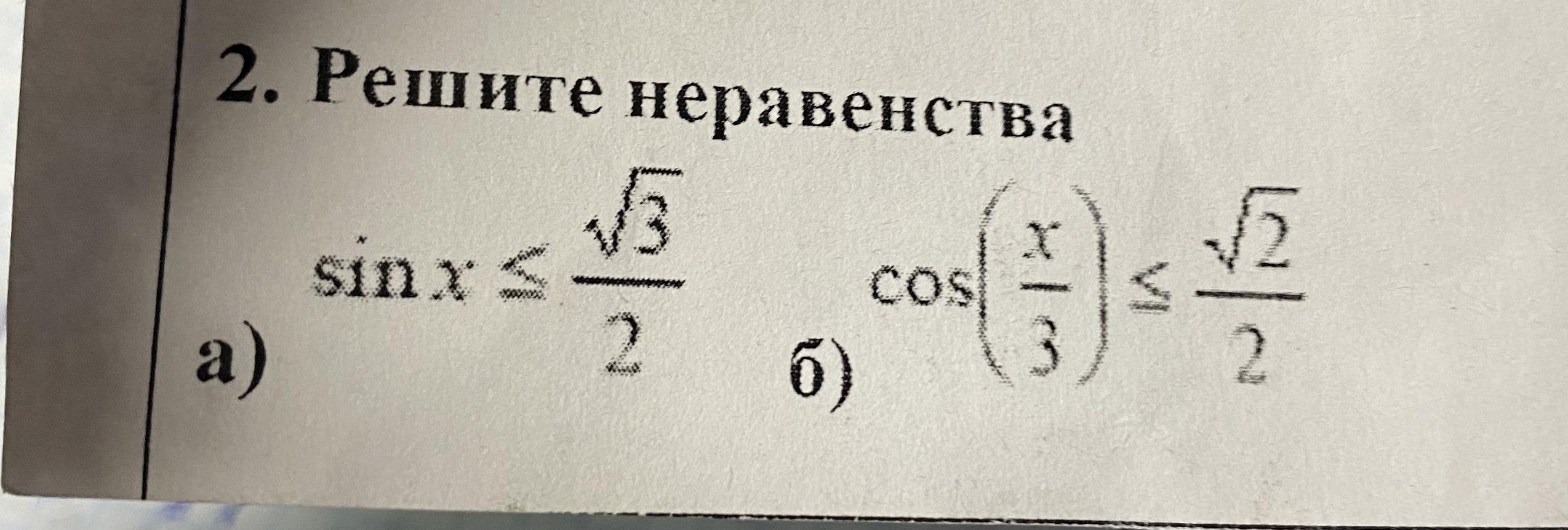
Ответы
Автор ответа:
1
Ответ:
Объяснение:
a) на единичной окружности проводим прямую у=V3 /2 параллельно оси
ОХ и решение -
это все точки окружности ниже этой прямой,
-4p/3<=x<=7p/3 и добавляем период 2pn, -4p/3 +2pn<=x<=7p/3 +2pn.
б) также проводим прямую х=V2/2 параллельно оси ОУ, решение
слева от этой прямой, p/4<=x/3<= 7p/4, p/4 +2pn<= x/3<=7p /4 +2pn,
умножаем все на 3, 3p /4 +6pn<=x<=21p/ 4 +6pn, n E Z
Автор ответа:
0
а)
, n∈Z
, n∈Z ⇔
⇔ , n∈Z
Ответ: , n∈Z
б)
, n∈Z
, n∈Z
, n∈Z
Ответ: , n∈Z
Похожие вопросы
Предмет: Русский язык,
автор: morgoslepoviv
Предмет: Другие предметы,
автор: karinakarpovic
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: мана8
Предмет: Литература,
автор: baydoolot08owo3ao