Предмет: Алгебра,
автор: DinaAssylbekova
Дробно-линейная функция задана уравнением: f(x)=(ax+11)/(2x+b)
a) Асимптоты функции имеют уравнения x=2, y=3. Найдите значение переменных a и b.
b) Используя результаты предыдущего действия:
i) приведите функцию f(x)=(ax+11)/(2x+b) к виду =n+k/(x+n);
ii) найдите точки пересечения функции с осями координат;
iii) постройте график функции.
DeLaFere:
В пункте а) перед =2 и =3 должно же что-то быть?
Х=2 и У=3
Большое задание. Буду пробовать.
Спасибо
Ответы
Автор ответа:
4
Ответ:
Объяснение:
а) х=2 это вертикальная асимптота. Это точка разрыва, т. е. это будет та точка, в которой знаменатель равен 0, т.к. на 0 делить нельзя. Следовательно
2·2+b=0; b=-4
y=3 - это горизонтальная асимптота. К этому значению стремится предел функции. Тогда
Применяя правило Лопиталя, будем иметь
b)
i)
Как видим, к требуемому виду функция не приводится, т.к. 3≠-2
ii) В точках пересечения с осью у абцисса равна 0. Подставляем в уравнение, находим у:
A(0;-2.75) - точка пересечения с осью у
В точках пересечения с осью х ордината равна 0. Решаем уравнение
- точка пересечения с осью х.
iii) Дополнительно исследуем функцию в точке разрыва
Схематически строим график
Приложения:
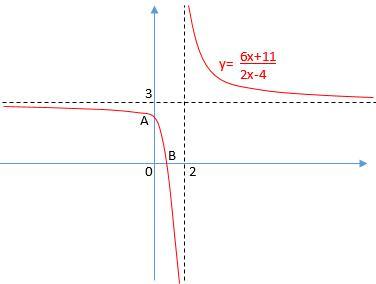
в пункте а) ошибка была. Исправил.
Огромное вам спасибо
Что-то с графиком неправильно. Там же у А отрицательная координата получилась(( Надо переделывать.
Здесь уже не могу изменить ответ. Задай последнее задание еще раз, там отвечу.
Похожие вопросы
Предмет: Русский язык,
автор: creedn
Предмет: Русский язык,
автор: mama11234154
Предмет: Қазақ тiлi,
автор: syrym3698
Предмет: История,
автор: maxitomko
Предмет: Литература,
автор: nmtsl