Предмет: Алгебра,
автор: vladgorbkov
Помогите с алгеброй, умоляю, даю 30 баллов
Приложения:
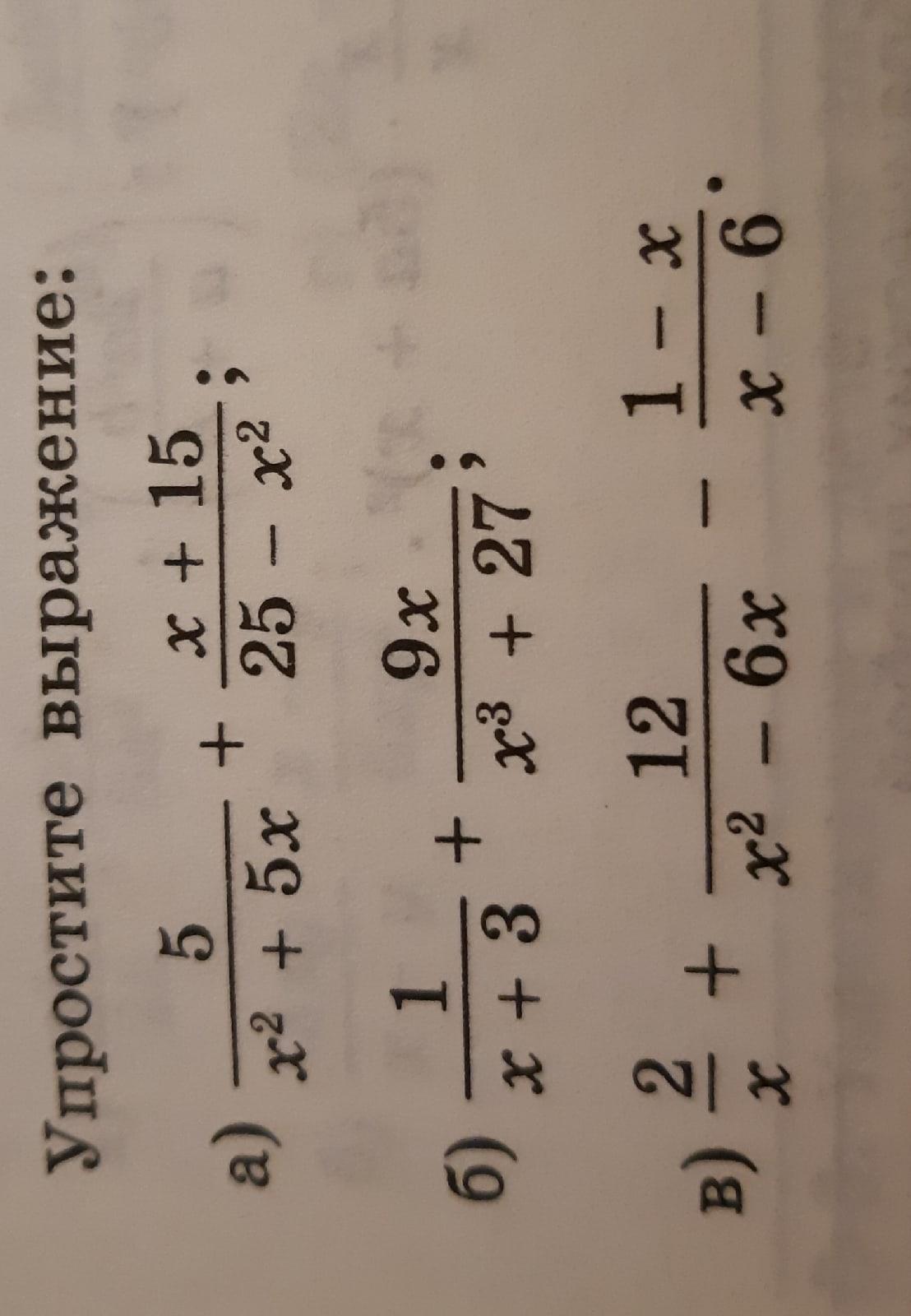
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: artemqqq
Предмет: Русский язык,
автор: sergejshirin
Предмет: Русский язык,
автор: mitrova0209
Предмет: Математика,
автор: Диляра575
Предмет: Математика,
автор: dariaromanova5380