Question

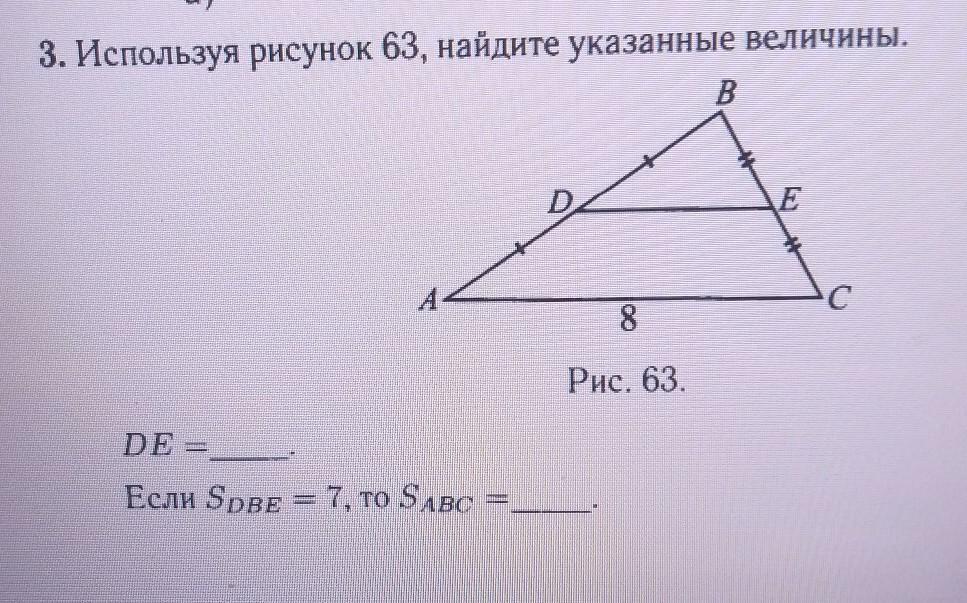
Найдите указанные величины Используя рисунок 63​

Answer 1

Дано :

ΔАВС.

D - середина АВ (AD = BD), E - середина BC (BE = CE).

AC = 8 (ед), $S\triangle _{DBE}$ = 7 (ед²).

Найти :

DE = ? ; $S\triangle _{ABC}$ = ?

Решение :

• Средняя линия треугольника - отрезок, соединяющий середины двух сторон треугольника.

Тогда DE - средняя линия ΔАВС по определению.

• Средняя линия треугольника в 2 раза меньше стороны, которой она параллельна.

Так как DE соединяет середины AB и BC, то DE║AC ⇒ DE = $\frac{1}{2}$AC = $\frac{1}{2} *8$ = 4 (ед).

• Средняя линия треугольника отсекает от него подобный треугольник с коэффициентом подобия в 2.

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

То есть $\frac{S\triangle _{ABC}}{S\triangle _{DBE}} = k^{2} = 2^{2} = 4$ ⇒ $\frac{S\triangle _{ABC}}{7} = 4$ ⇒ ${S\triangle _{ABC}= 7*4 = 28$ (ед²).

Ответ :

4 (ед), 28 (ед²).