Question

Составить уравнение гиперболы, симметричной относительно осей
координат, если она проходит через точки М1 (х1, у1) и М2 (х2, у2)
(таблица 3). Найти: 1) действительную и мнимую полуоси;
2) эксцентриситет. Построить гиперболу.
x1=1
x2=3
y1=2
y2=7

Answer 1

Даны точки М1 (1; 2) и М2 (3; 7).

Подставим эти координаты в уравнение гиперболы.

$\frac{1}{a^2} -\frac{4}{b^2} =1,\\\frac{x}{y} \frac{9}{a^2} -\frac{49}{b^2} =1.$

Получаем уравнение $b^2-4a^2=9b^2-49a^2,\\b^2=\frac{45}{8} a^2.$

Замена: подставим значение b^2 в первое уравнение.

(1/a^2) -(4/(45/8)a^2) = 1.

Отсюда находим a^2 = 13/45, а b^2 = (45/8)*(13/45) = 13/8.

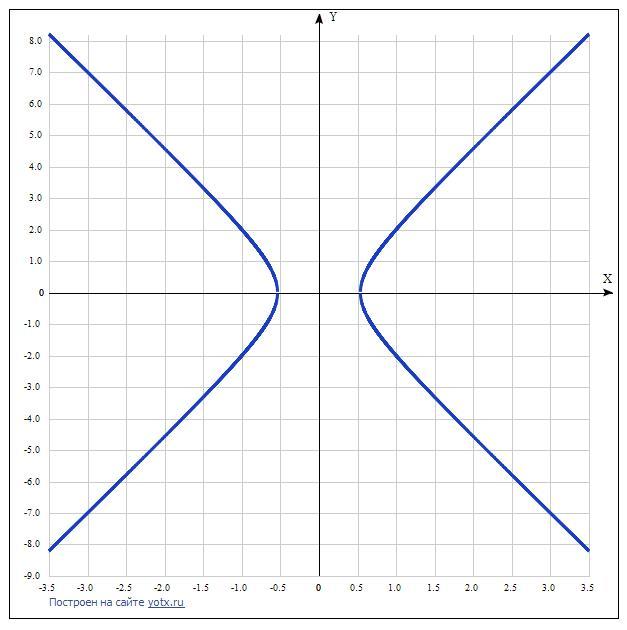
Ответ: уравнение гиперболы (x^2/(13/45)) - (y^2/(13/8)) = 1.

Параметры гиперболы и график приведены во вложении.