Question

помогите пж
срочно
даю 10баллов

Answer 1

Ответ:

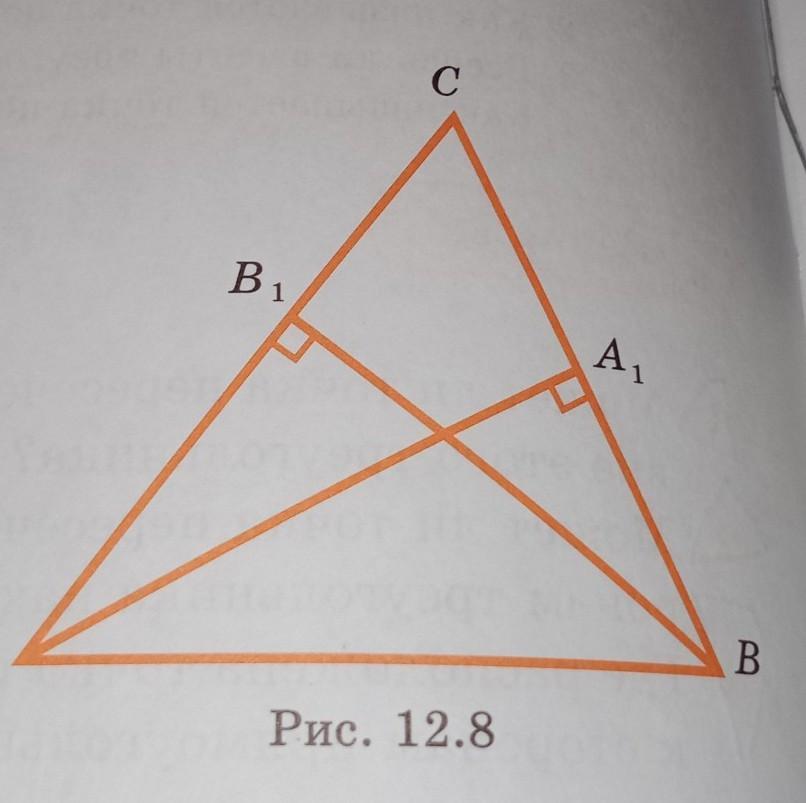
Итак, медианы b1b и A1A находятся в треугольниках b1ba и a1ab или в треугольниках b1bc и a1ac. Для доказательства равенства медиан надо доказать равенство треугольников.

Выбираем первую пару. Треугольники b1ba и a1ab. Поскольку треугольник CBA равнобедренный, то cb=ca.

Но медиана делит противоположную сторону треугольника пополам. Отсюда ab1=b1c=ca1=a1b. Или b1a=a1b.

Углы при основании равнобедренного треугольника равны. Получается ∠А=∠B. Теперь вернёмся опять к треугольникам AA1B и B1BA. У них AB1=A1B.

Угол A1BA равен углу B1BA, а сторона BA — общая.

Получается, треугольники равны по первому признаку равенства треугольников.

А в равных треугольниках против равных углов лежат равные стороны.

Против угла A1BA в треугольнике ABA1 лежит сторона A1A, а против угла B1AB в треугольнике BAB1 лежит сторона B1B. Значит, эти стороны равны.