Question

постройте график функции:
y=8-4x/x^2-2x.
помогите пожалуйста

Answer 1

Ответ:

Объяснение:

$y=8-\frac{4x}{x^2}-2x$

На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)

$\lim_{x \to +0} (8-\frac{4x}{x^2}-2x)=-\infty \\ \lim_{x \to -0} (8-\frac{4x}{x^2}-2x)=\infty$

Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.

$8-\frac{4x}{x^2}-2x=8-\frac{4}{x}-2x=\frac{8x-4-2x^2}{x}\\ \frac{8x-4-2x^2}{x}=0\\8x-4-2x^2=0\\x^2-4x+2=0$

Решаем квадратное уравнение, находим точки пересечения с осью х:

$x_1=2-\sqrt{2} \\x_2=2+\sqrt{2}$

Находим точки экстремума (производная равна нулю).

$(8-\frac{4x}{x^2}-2x)'=(8-\frac{4}{x}-2x)'=\frac{4}{x^2}-2;\\ \frac{4}{x^2}-2=0\\ \frac{2}{x^2}=1\\x=\pm \sqrt{2};\ \ y(-\sqrt{2})=8+4\sqrt{2};\ \ y(2)=8-4\sqrt{2}$

Для нахождения точек перегиба находим вторую производную

$y''=(\frac{4}{x^2}-2)'= (4x^{-2}-2)'=-\frac{8}{x^3}$

Вторая производная нигде не равна нулю, точек перегиба нет.

Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.

Ищем наклонную асимптоту:

$k= \lim_{x \to \pm \infty} \frac{f(x)}{x}= \lim_{x \to \pm \infty} (\frac{8}{x}-\frac{4}{x^2}-2 )=-2$

$b= \lim_{x \to \pm \infty} (f(x)}-k{x})= \lim_{x \to \pm \infty} (8-\frac{4}{x}-2x+2x )=8$

Наклонная асимптота есть:

$y=-2x+8$

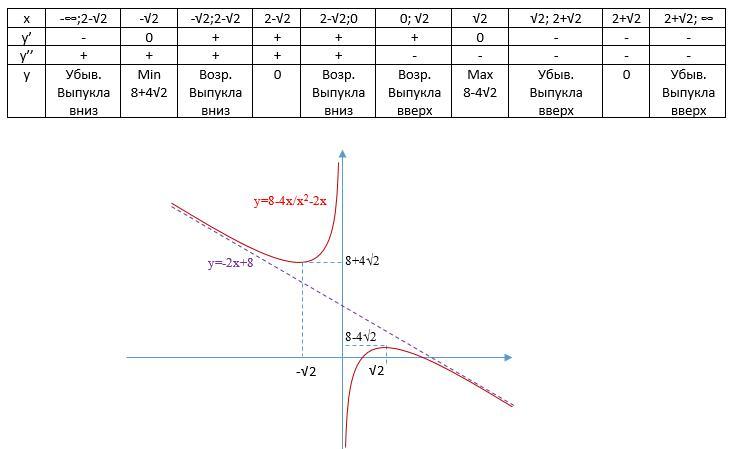
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).