Question

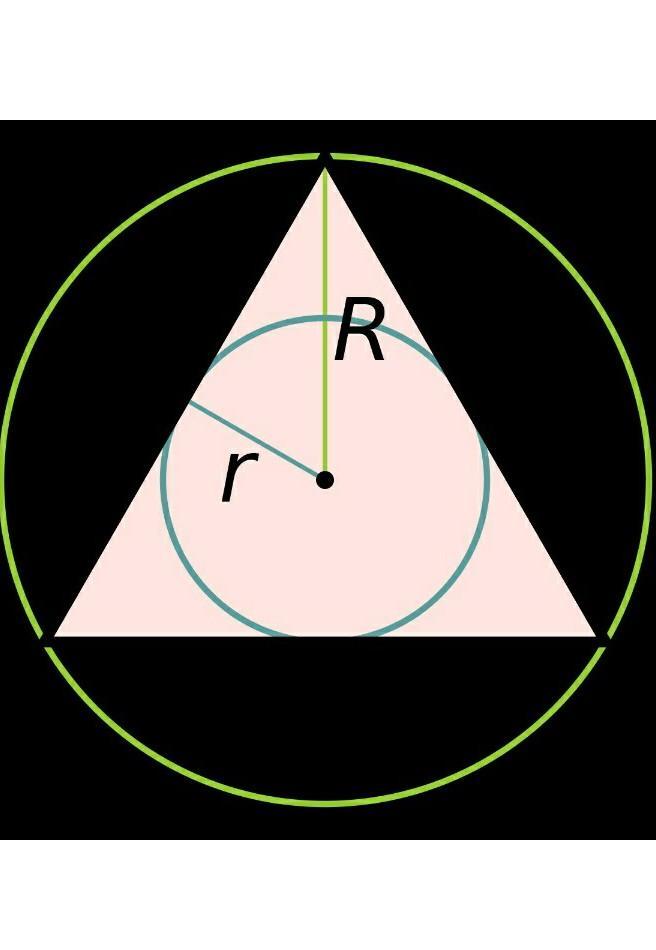
Радиус окружности, описанной около правильного треугольника на 2√3 больше радиуса вписанной в этот треугольник окружности. Найдите длину стороны треугольника.

Answer 1

Ответ:

сторона треугольника 12

Объяснение:

формула нахождения радиуса описанной окружности:

$R= \frac{a}{ \sqrt{3} }$

формула нахождения радиуса вписанной окружности:

$r = \frac{a}{2 \sqrt{3} }$

где а - сторона треугольника, R - радиус описанной окружности, r - радиус вписанной окружности

Так как радиус описанной окружности больше вписанной, и зная их разницу составим уравнение:

$\frac{a }{ \sqrt{3} } - \frac{a}{2 \sqrt{3} } = 2 \sqrt{3}$

находим общий знаменатель:

$\frac{2a - a}{2 \sqrt{3} } = 2 \sqrt{3}$

$\frac{a}{2 \sqrt{3} } = 2 \sqrt{3}$

перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:

а=(2√3)²=4×3=12

Итак: сторона а= 12

Проверка: радиус описанной окружности=

$\frac{12}{ \sqrt{3} }$

радиус вписанной окружности:

$\frac{12}{2 \sqrt{3} } = \frac{6}{ \sqrt{3} }$

теперь вычтем их разницу

$\frac{12}{ \sqrt{3} } - 2 \sqrt{3} = \frac{12 - 2 \sqrt{3} \times \sqrt{3} }{ \sqrt{3} } = \frac{12 - 2 \times 3}{ \sqrt{3} } = = \frac{12 - 6}{ \sqrt{3} } = \frac{6 }{ \sqrt{3} }$