Предмет: Алгебра,
автор: murodillaumarjonov
Прошу помочь привести к общему знаменателю. 20 баллов
Приложения:
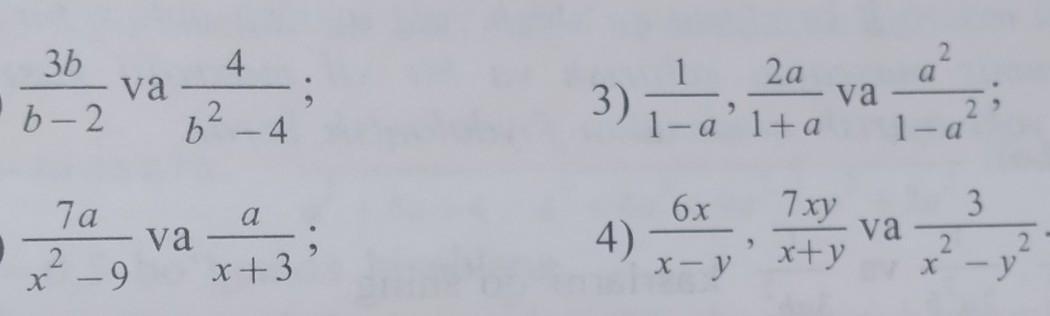
Ответы
Автор ответа:
1
Автор ответа:
1
1. 3b/(b-2)=3b*(b+2)/(b²-4)=(3b²+6b)/(b²-4); 4/(b²-4);
2. a/(х+3)=а*(х-3)/(х²-9)=(ах-3а)/(х²-9); 7а/(х²-9);
3. (1+а)/(1-а²); 2а*(1-а)/(1-а²)=(2а-2а²)/(1-а²); а²(1-а²);
4. (6х²-6ху)/(х²-у²); 7ху*(х-у)/(х²-у²)=(7х²у-7ху² )/(х²-у²); 3/х²-у²);
murodillaumarjonov:
спс
Похожие вопросы
Предмет: Русский язык,
автор: masha363
Предмет: Русский язык,
автор: z1ann2a
Предмет: Английский язык,
автор: haitovakristin
Предмет: Математика,
автор: NikiTosPLOT