Предмет: Математика,
автор: kamilamirahmatova
5.Стороны данного треугольника равны соответственно
12 см, 20 см и 13 см. Найдите стороны треугольника,
подобного данному, если меньшая его сторона равна
9 см.
Ответы
Автор ответа:
95
Дано: AB = 12см
BC = 13см
AC = 20см
A₁B₁ = 9см
Найти: B₁C₁
A₁C₁
Решение:
По третьему признаку подобия треугольников: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то они подобны.
Если , то Δ ABC ~ Δ A₁B₁C₁
Подставим значения сторон треугольника, которые уже знаем
Теперь найдём стороны B₁C₁ и A₁C₁
Ответ: A₁B₁ = 9см
B₁C₁ = 9,75см
A₁C₁ = 15см
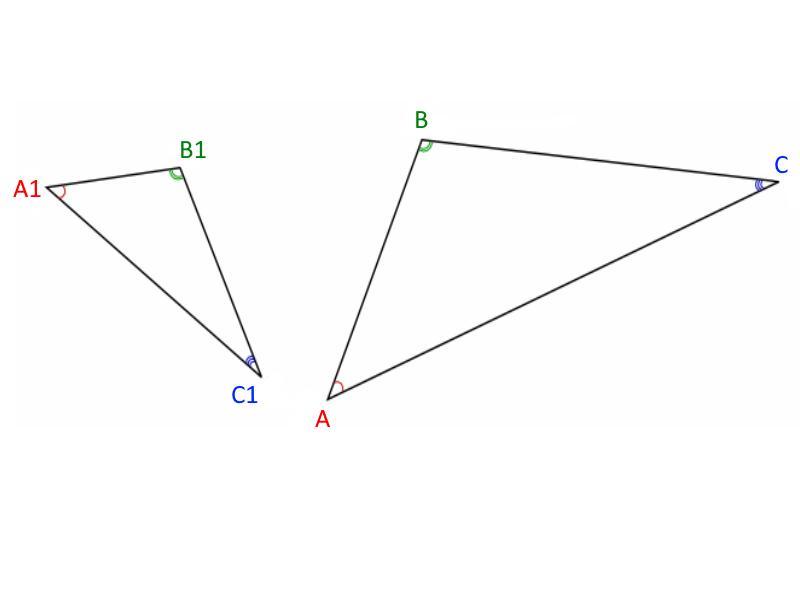
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: oxanakudryasho
Предмет: Русский язык,
автор: фрося12345
Предмет: Английский язык,
автор: Eviscerator
Предмет: Математика,
автор: KotofeykaLini
Предмет: Математика,
автор: nikfol