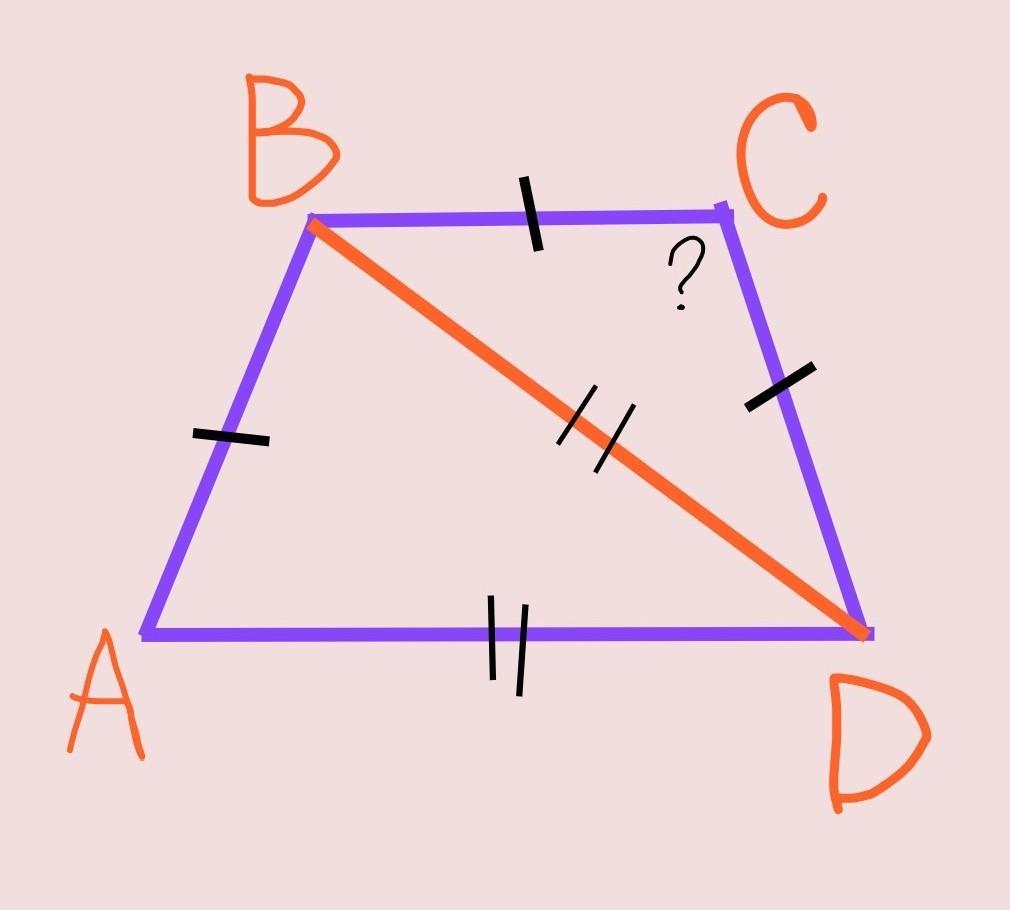
Три стороны AB, BC, CD трапеции ABCD равны. Диагональ BD равна основанию AD. Найдите угол BCD. Помогите пж потому, что везде просто копируют решение (при чëм не правильное) и я вообще в тупике. Не понимаю как это решать. Знаю только то, что нужно составить уравнение, но проблема: Как?
Ответы
Объяснение:
Так как BС=СD по условию, то ∆BCD – равнобедренный с основанием BD. Следовательно угол СВD=угол CDB как углы при основании равнобедренного треугольника.
Сумма углов любого треугольника равна 180°.
Исходя из этого угол ВСD=180°–угол CBD–угол СDB=180°–x–x=180°–2x
Пусть угол СВD=x, тогда угол CDB=х так же.
Основания трапеции параллельны, тоесть ВС//AD.
Тогда угол CBD=угол ADB как накрест лежащие при параллельных прямых ВС и AD и секущей BD.
Так как СВD=x, то угол ADB=x так же.
Так как BD=AD по условию, то ∆АВD – равнобедренный с основанием АВ. А углы при основании равнобедренного треугольника равны. Сумма углов в любом треугольнике равна 180°.
Исходя из этого: угол ABD=(180°–угол ADB)÷2=(180°–x)÷2
Угол АВС=угол ABD+угол CBD=(180°–x)÷2+x
Так как АВ=CD по условию, то трапеция ABCD – равнобедренная.
Углы при основании равнобедренной трапеции равны, тоесть: угол АВС=угол BCD.
Подставим величины этих углов, получим уравнение:
(180–x)÷2+x=180–2x
90–0,5х+х=180–2х
–0,5х+х+2х=180–90
2,5х=90
х=36
Тогда угол ВСD=180°–2*36°=108°
Ответ: 108°