Question

Мне под (7)
Помогите пожалуйста

Answer 1

Ответ:

Пошаговое объяснение:

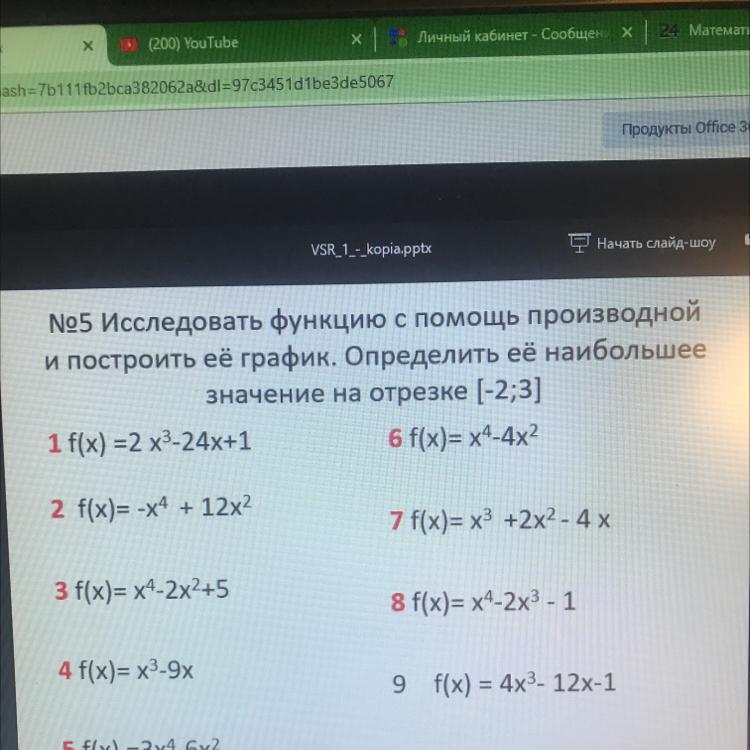
f(x)=x³+2x²-4x;

1, Область определения х∈(-∞;+∞). Функция непрерывна на всей числовой оси. Т.е. точки разрыва отсутствуют.

2. Попробуем найти точки пересечения с осями абсцисс и ординат:

с осью ОХ (там, где у=0):

x³+2x²-4x=0;

x(x²+2x-4)=0;

x₁=0;

x²+2x-4=0; D=4+16=20; x₂₃=0,5(-2±2√5); x₂₃=-1±2,24;

x₂=1,24; x₃=-3,24

С осью ОУ (там, где х=0):

у=x³+2x²-4x; x=0;

y=0+0-0=0.

3. Найдем точки экстремумов:

y'=(x³+2x²-4x)';

y'=3x²+4x-4;

y'=0; 3x²+4x-4=0; D=16+48=64; x₁₂=1/6*(-4±8);

абсциссы точек-экстремумов: x₁= -2; x₂=2/3≈0,67

для определения характера экстремума (min, max) найдем вторую производную:

y''=(y')'=(3x²+4x-4)'=6x+4;

определим знак второй производной в точках экстремума:

y''(-2)=6*(-2)+4<0 точка максимума

y''(2/3)=6*(2/3)+4=-4>0 - точка минимума

Ординаты экстремумов y=x³+2x²-4x:

y_max=y(x₁)=y(-2)=(-2)³+2*(-2)²-4*(-2)= -8+8+8=8

y_min=y(x₂)=y(2/3)=(2/3)³+2*(2/3)²-4*(2/3)=8/27+8/9-8/3=(8+24-72)/27=

=-40/27≈-1,48

Итак, вот по этим данным строим график:

точки пересечения с осью ОХ:

(0;0), (0;1,24), (0;-3,24)

точки пересечения с ОУ

(0;0)

точки экстремумов:

минимум: (0,67;-1,48),

максимум: (-2;8)

Максимальные (минимальные) значения фунции на отрезке (промежутке) находятся  или на концах промежутка, или в точках экстремумов, которые существуют на данном промежутке.

Заданный отрезок [-2;3]; f(x)=x³+2x²-4x;

Находим значения функции по концам промежутка:

y(-2)= +8 - уже вычисленная точка максимума

y(3)=3³+2*3²-4*3=27+18-12=33;

Максимальное зачение: в т (3;33)

минимальное значение в т.минимума: (0,67;-1,48)