Предмет: Геометрия,
автор: Ktototypoi
Задания на карточках. Помогите, пожалуйста, как можно скорее решить, завтра сдавать надо, а я затрудняюсь с решением. И да, будьте добры, чертёж тоже сделайте. Заранее огромное спасибо)
Приложения:

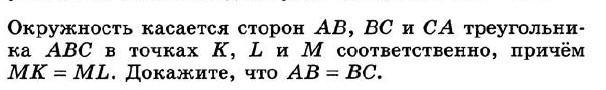
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
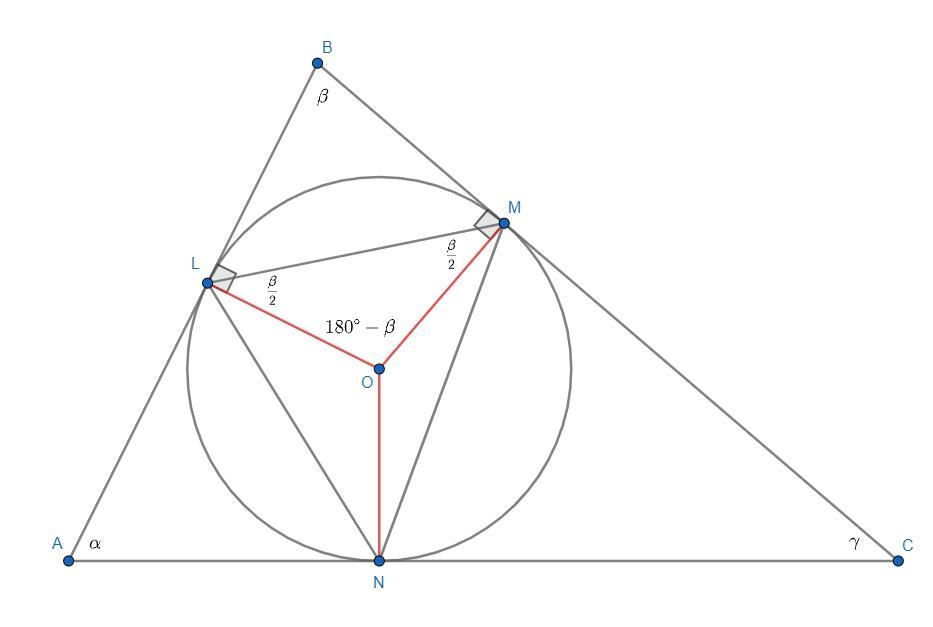
Проведем два радиуса OL и OM к касательным в точку касания. Тогда. Значит
. Т.к. OL=OM - радиусы, то ΔLOM - равнобедренный, а значит
. Аналогично получаем, что
и
.
Тогда ,
,
. При
,
,
,
,
,
.
Задача решена!
Приложения:
Ktototypoi:
Спасибо большое, солнце! Ты меня очень выручил(а)! ❤️
Кстати, а скажи-ка, пожалуйста, к какой карточке относится , приведённое тобой решение?
Похожие вопросы
Предмет: Русский язык,
автор: lalaka03
Предмет: Английский язык,
автор: Дергачува
Предмет: Русский язык,
автор: borkovchenkov2
Предмет: История,
автор: sultanovaz236